Le sujet du Controle continu 15-16 corrige

!"#!$%&'()*+,-%.-)%/012.-)%34256*42)%.-)%40/12*)7-)%8*8126)%
!"#$%&'()*"#$+#,)-).)#"/(01%()2345)6)*"%%+78)
Durée&:&2h.&Documents&interdits.&Dans&les&exercices,&pour&chaque&question,&donner&une&formule&littérale&avant&de&faire&
l’application&numérique.&Toute&grandeur&physique&doit&être&donnée&avec&ses&unités.&
1)#EXERCICE#:#Rétrécissement#d’une#aorte.#
%
92%-:17-2%;5'4<.4==>-0%=-07-6%.-%7-),0-0%>-)%8*6-))-)%V$%-6%V!%.,%)12/%>-%>42/%.?,2-%106@0-%-6%-2%
5400-)=42.125-%.?*2%0;60;5*))-7-26%A84*0%3*/,0-B%C%
V$%%D%$%7E)%
V!%%D%F%7E)%
G-%.*17@60-%.-%>?106@0-%-2%S$%-)6%1,))*%7-),0;%=10%;5'4/01='*-%C%
d$%D%!H%77I%
$B 96*>*)-0%>1%542)-0816*42%.,%.;J*6%=4,0%51>5,>-0%>-%.*17@60-%d!%1,%2*8-1,%.,%0;60;5*))-7-26K%=,*)%>-%01==406%
.-)%),0315-)%S!ES$I%
Le débit Q s’écrit Q = ∆Vol/∆t avec ∆Vol le volume qui traverse une section donnée pendant un temps ∆t.
En écrivant ∆Vol = S ∆x puis la longueur ∆x = V ∆t on peut récrire Q = S V.
La conservation du débit s’écrit alors Q1 = S1V1 = S2V2, d’où
S2/S1 = V1/V2 = ¼
et puisque S = πd2/4, on trouve d22 /d12 = ¼ , d2/d1 = ½ et finalement d2 = ½ d1 = 10 mm.
!B L2%),==4)126%+,-%>-)%-33-6)%.-%8*)54)*6;%)4*-26%*5*%2;/>*/-1J>-)K%>-%6';40@7-%.-%M-024,>>*%)?1==>*+,-%-6%
=-07-6%.?;50*0-%%%
€
1
2
ρ V2+P=cte
%%
>-%>42/%.-%>?106@0-K%18-5% ρ %N%$HOH%P/E7!%1%71))-%84>,7*+,-%.,%)12/K%V%)1%8*6-))-%-6%P%)1%=0-))*42I%%
Q==>*+,-0%>-%6';40@7-%=4,0%51>5,>-0%>1%=0-))*42%P$%%-2%17426%.,%0;60;5*))-7-26%A-2%S$B%)*%>1%=0-))*42%P!%-)6%
.-%RH%77S/I%
½ ρ V12 + P1 = ½ ρ V22 + P2
P1 – P2 = ½ ρ ( V22 – V12 ) = ½ 1060 kg m-2 ( 16 - 1 ) m2 s-2 = 7950 Pa
or 105 Pa = 760 mmHg : donc 7950 Pa = (7950 *760 / 105 ) mmHg = 60 mmHg.
Finalement, on a donc P1 = P2 + 60 mmHg = 150 mmHg.
#B T,-%81,6K%.12)%>-)%7U7-)%'(=46'@)-)K%>1%=0-))*42%-2%181>%.,%0;60;5*))-7-26%V%
La pression en aval ou en amont est la même, car le théorème de Bernouilli s’applique de la même manière tout le long d’une ligne de
flux du fluide en écoulement. On trouverait donc la même valeur que P1.

!"#!$%&'()*+,-%.-)%/012.-)%34256*42)%.-)%40/12*)7-)%8*8126)%
2)#ANALYSE#:#cycle#cardiaque.#
%
W12)%>-)%604*)%3*/,0-)%5*<.-))4,)K%,2%5(5>-%=0-))*42<84>,7-%54260X>-%A-2%/0*)B%-)6%547=10;%Y%604*)%5(5>-)%
510156;0*)6*+,-)%.-%604*)%=16'4>4/*-)%510.*1+,-)%.*33;0-26-)%C%,2-%510.*47(4=16'*-%.*>16;-K%,2-%'(=-0604='*-%
8-260*5,>1*0-%/1,5'-%-6%,2%0;60;5*))-7-26%1406*+,-K%0-)=-56*8-7-26I%W12)%>-)%604*)%3*/,0-)K%42%6015-%>1%=0-))*42%
8-260*5,>1*0-%/1,5'-%AG"&B%-2%34256*42%.,%84>,7-%8-260*5,>1*0-%/1,5'-%AG""BI%
Q%=106*0%.-)%3*/,0-)K%5477-26-Z%>-%0X>-%.*1/24)6*5%.-%5-%/-20-%.-%.*1/0177-%-6K%)*%84,)%>-%)4,'1*6-ZK%),0%>-)%
-33-6)%.-)%=16'4>4/*-)%542)*.;0;-)I%%
Une&page&maximum.&
Le diagramme pression-volume permet de décrire le comportement du cœur au cours d’un cycle, et notamment de visualiser le volume
de sang expulsé (différence entre les valeurs maximale et minimale du volume LVV) et les pressions exercées. De plus, il permet d’avoir
une mesure directe du travail fourni par le cœur, qui correspond à la surface contenue dans le cycle.
En cas de comportement pathologique, la comparaison entre le diagramme observé et le diagramme de référence pour un cœur sain
donnent également des informations immédiates sur le type de défaillance. Par exemple, dans le cas de la cardiomyopathie dilatée, on
observe une augmentation à la fois du volume minimal et du volume maximal du ventricule, sans une grande altération des pressions :
on peut donc en conclure que le ventricule est plus grand que dans le cas normal, ce qui peut être dû à une relaxation du muscle
cardiaque. Dans le cas de l’hypertrophie ventriculaire, on observe au contraire une réduction du volume total de sang éjecté, due à une
réduction du volume maximal et une augmentation du volume minimal. En association avec ces modifications, on observe une
augmentation de la pression maximale enregistrée dans le ventricule. Ces données sont compatibles avec l’hypothèse d’une
hypertrophie du muscle cardiaque qui, gonflé, d’une part réduit son volume interne, d’autre part perd probablement en élasticité.
L’augmentation de pression apparaît alors comme une conséquence de cette réduction du volume accessible, de cette « manque de
place ». Dans le troisième cas présenté on parle de rétrécissement aortique : on imagine donc que l’expulsion du sang à la contraction
ventriculaire est contrée par un conduit de sortie insuffisamment large. Les conséquences observées dans le diagramme semblent
logiques car on observe une augmentation de la pression, d’une part, et une augmentation du volume ventriculaire minimal, d’autre
part : on peut en déduire que le sang, empêché de sortir, ne vide pas complètement le ventricule, et exerce une pression augmentée car
la contraction du muscle cardiaque est toujours aussi efficace que dans le cas d’un cœur sain.

!"#!$%&'()*+,-%.-)%/012.-)%34256*42)%.-)%40/12*)7-)%8*8126)%
3)#EXERCICE#:#Rein#artificiel.#
92%%.*)=4)*6*3%.-%0-*2%106*3*5*->%-)6%542)6*6,;%.-%.-,:%
547=106*7-26)%);=10;)%=10%,2-%7-7J012-%.?;=1*))-,0%eK&
=-07;1J>-%Y%>?,0;-I%%
W12)%,2%.-)%547=106*7-26)%5*05,>-%>-%)12/K%.426%>1%
5425-26016*42%-2%,0;-%-)6%CsI%%
W12)%>?1,60-%547=106*7-26%,2%3>,:%5426*2,%.-%)4>,6*42%=-07-6% .-%
71*26-2*0%>1%5425-26016*42%.?,0;-%Y%,2-%81>-,0%2;/>*/-1J>-K%Cext = 0I%
G1%.-,:*@7-%>4*%.-%[*5PK%
%
=-07-6%.-%51>5,>-0%>1%5425-26016*42%-2%,0;-%Y%6018-0)%>1%
7-7J012-%-2%54221*))126%)-)%81>-,0)%1,:%.-,:%J40.)%C%x = 0&et&x = e.&
&
$B \*7=>*3*-0%>1%.-,:*@7-%>4*%.-%[*5P%-2%542)*.;0126%+,-%>-%)()6@7-%-)6%-2%0;/*7-%)616*4221*0-I%
En régime stationnaire la concentration ne change pas au cours du temps, donc la dérivée est nulle : ∂C / ∂t = 0. Il en suit :
0 = ∂2C / ∂x2.
2) ]4260-0%+,-%>1%)4>,6*42%.-%>?;+,16*42%.-%[*5P%4J6-2,-%-2%A$B%-)6%,2-%>4*%>*2;1*0-K%C(x) = A x + B&
La dérivée seconde par rapport à x de C(x) = Ax+B est nulle, donc on a bien 0 = ∂2C / ∂x2.
#B L50*0-%-:=>*5*6-7-26%>-)%542.*6*42)%1,:%J40.)%C%C(0)%-6%C(e).%
En suivant ce qui est expliqué dans le sujet on a C(0) = CS, C(e) = Cext = 0.
FB W;6-07*2-0%>-)%542)6126-)%A%-6%B%+,*%=-07-66-26%.-%)16*)31*0-%>-)%542.*6*42)%1,:%J40.)I%
En utilisant les conditions au bord, on peut écrire :
C(0) = A•0+B = B = CS
C(e) = A•e+B = 0
d’où B = CS, et A = - CS / e
^B _015-0%>1%5425-26016*42%C(x)%-2%34256*42%.-%xI%
En remplacent, on a C(x) = CS (1 – x/e). On peut vérifier qu’on a bien C(0) = CS et C(e) = 0.
OB T,-%81,6%>-%3>,:%.?,0;-K%%%%
%%V%
En dérivant C(x) on a ∂C(x) / ∂x = A = - CS/e, d’où
j = D CS /e.
On peut vérifier que j > 0, ce qui est compatible avec une concentration en urée plus haute en x>0 que en x>e.
!
" C
" t(x,t)=#D
"
2C
" x2(x,t)
!
j(x,t)="D
# C
# x(x,t)
x&
0&&&&e&
Cs%
Cext%

!"#!$%&'()*+,-%.-)%/012.-)%34256*42)%.-)%40/12*)7-)%8*8126)%
4)#EXERCICE#:#Equilibre###
92%'477-%)-%6*-26%.-J4,6K%),0%,2-%)-,>-%`17J-I%a>%-)6%)4,7*)%Y%.-,:%
3405-)%C%)42%=4*.)% %-6%>1%0;156*42 %.,%)4>I%G1%=4)*6*42%.-%>1%`17J-%
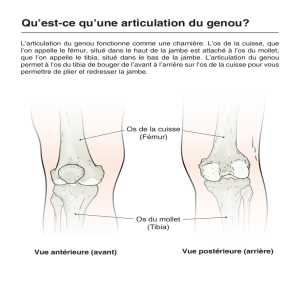
.b1==,*%=-,6%U60-%)5';716*);-%5477-%),0%>1%3*/,0-%5*<.-))4,)%C%>-%
)-/7-26%QM%0-=0;)-26-26%>b;=*='()-%),=;0*-,0-%.,%3;7,0K%.b,2-%
>42/,-,0%.-%c%57%d%e%-)6%>-%=4*26%.b1==,*%),0%>-%)4>%-6%W%>-%5-260-%.-%
/018*6;%.-%>1%`17J-I%%
$I G1%71))-%.-%5-6%'477-%-)6%.-%fH%P/I%T,-%81,6%g%V%
La réaction du sol R doit équilibrer le poids pour que l’homme soit à l’équilibre : donc, R =
mg ≅ 700 N.
!I G1%71))-%.-%>1%`17J-%-)6%.-%$H%P/I%\,0%>1%3*/,0-K%0-=0;)-26-Z%)42%
=4*.)% I%h,)6*3*-ZI%
Le poids est Pj = mj g ≅ 100 N, vers le bas, et son point d’application est au centre de
gravité de la jambe, point D (vecteur en bleu).
#I _015-Z%A-6%`,)6*3*-Z%84)%6015;)%)4*/2-,)-7-26K%246177-26%>-)%2407-)%
.-)%8-56-,0)B%C%
i >1%3405-%-:-05;-%=10%>-)%7,)5>-)%1..,56-,0)%),0%>-%/012.%
6045'126-,0%.,%3;7,0K%1,%=4*26%QI%L>>-%31*6%,2-%12/>-%.-%O^j%
18-5%>b'40*Z4261>-K%
Vecteur en rouge
i >1%3405-%-:-05;-%=10%>-%J1))*2%),0%>1%6U6-%.,%3;7,0K%)b-:-0k126%
1,%=4*26%MI%
Vecteur en vert
!1+!2+"#+$=0
Les projections verticales donnent donc F1h + F2h = 0 et F1v + F2v + Pj + R = 0
et de plus (AB)h.F1v + (BD)h.Pj + (BC)h.R = 0 i.e. 0,08 F1v + 0,02 Pj = 0,1R
%&4,0%7;74*0-K%,2-%0-=0;)-2616*42%)5';716*+,-%.-%>1%6U6-%.,%3;7,0%-)6%
.422;-%5*<.-))4,)%C%%
Q3*2%.-%)4,>1/-0%5-66-%106*5,>16*42K%2460-%'477-%)b1*.-%.b,2-%5122-%,6*>*);-%),%5X6;%4==4);%Y%5->,*%.-%>1%`17J-%
.b1==,*I%e-66-%=4)*6*42%-)6%0-=0;)-26;-%5*<.-))4,)I%L:=>*+,-Z%+,1>*616*8-7-26%=4,0+,4*%-)6<5-%+,-%>-)%7,)5>-)%
1..,56-,0)%.,%J1))*2K%5477-%>1%6U6-%.,%3;7,0K%)426%/012.-7-26%)4,>1/;)I%
^I _015-Z%,2%)5';71%.-%3405-)%;+,*81>-26%Y%5->,*%+,-%84,)%18-Z%547=>;6;%
=4,0%>-%51)%24071>%71*)%5-66-%34*)%-2%6-2126%547=6-%.-%>b-33-6%.-%>1%
5122-I%
%%
%
G1%5122-%)-06%.b1==,*)K%-6%,2-%547=4)126-%g!%.-%>1%0;156*42%.,%)4>%-)6%6->>-%
+,-%$1+$2+"=0 Ag!%l!H%m%.-%=4*.%.,%540=)BI%e->1%81%J*-2%1,<.->Y%.b,2-%
)*7=>-%.*7*2,6*42%.,%=4*.%.,%540=)%-:-05;%),0%>-%=*-.I%G-%5426156%.-%>1%5122-%
18-5%>-%)4>%A=4*26%WB%-)6%Y%l#H%57%.-%>b1:-%.,%540=)%-6%42%1%C%
%& ∧ $1+%' ∧ $2=05-%+,*%.422-%,2-%0;=106*6*42%.-)%3405-)%60@)%
.*33;0-26-%n%
%

!"#!$%&'()*+,-%.-)%/012.-)%34256*42)%.-)%40/12*)7-)%8*8126)%
[*/,0-)%5400-56*42%C%84*0%5*<.-))4,)%
%
lO57%
g$%
g!%