Electrophorèse sur support

Cnam Paris, Electrochimie Industrielle - Travaux pratiques B1, N°5
1
_______________________________________________________________________
Manipulation N°5 Electrophorèse sur support
_______________________________________________________________________
1. BUT DE LA MANIPULATION:
• Déterminer le point isoélectrique d’un acide aminé par électrophorèse.
• Détermination de la mobilité des cations minéraux Ag+ et Cu2+.
2. PRINCIPE:
On appelle électrophorèse, la migration d'une substance dissoute ou en suspension dans un
solvant sous l'action d'un champ électrique. Elle peut avoir lieu en phase liquide ou sur un
support imprégné d'un électrolyte support convenablement choisi.
L'électrophorèse peut être utilisée à des fins de chimie préparatrice ou analytique, et dans ce
dernier cas, à des buts, tant qualitatifs que quantitatifs.
Un acide α-aminé a la formule suivante:
R CH COOH
NH2
Lorsqu'il ne possède qu'une seule fonction de chaque nature.
En solution aqueuse, il se présente comme un mélange de différentes formes ionisées:
RCH COOH
N
H3
+
RCH COO
N
H2
-
RCH
N
H3
+COO-
: cation
: anion
: zwitterion ou ion hybride, électriquement neutre
La forme prédominante et, par conséquent, le sens de migration de l'acide aminé dépendent
donc du pH de la solution.

Cnam Paris, Electrochimie Industrielle - Travaux pratiques B1, N°5
2
Chaque acide aminé est caractérisé par son point isoélectrique PI qui correspond à la valeur
du pH pour laquelle son transport dans un champ électrique est nul, c'est-à-dire, le pH pour
lequel il est électriquement neutre.
On peut donc considérer qu'au point isoélectrique, la molécule est presque totalement
dissociée en ions mixtes, produits par migration d'un proton d'une extrêmité de la chaîne à
l'autre:
R CH COOH
NH2
R CH
NH3
+COO-
Dans le cas étudié (acide glutamique), la molécule présente deux fonctions carboxyliques et un
groupement aminé:
C CH2CH C
NH2
O
OH
CH2
O
OH
Selon le pH de la solution dans laquelle elle sera dissoute, on pourra admettre qu’elle existera
sous l’une des formes prédominantes suivantes:
AH3
+AH2AH-A- -
,,,
±
Il conviendra donc d’envisager les équilibres suivants:
H+
+
AH3
+AH2
-+K3pK3= 2,1
H+
-
AH2
+AH +K2pK2= 4,1
-
H
AH A +K1pK1= 9,5
-2-
et de remarquer que si C0 est la concentration en acide aminé, il vient:
3
= (AH ) +
0-+
C (AH ) (A )
+
-2-
2
(AH ) +
+

Cnam Paris, Electrochimie Industrielle - Travaux pratiques B1, N°5
3
soit encore:
2
(H )
0-
+
C+
2
[AH ]
+
=K1K2
(H )
++
K21+ H+
K3
ou bien:
2
(H )
++
K1K2
(H )
++
K21+H
K
0- C
2
AH =
+
3
+
Le point isoélectrique est le pH pour lequel (AH2±) prends sa valeur maximale. Dans ces
conditions:
d(H )
+= 0
-
2
d(AH )
+
et pH iso = 1/2 (pK2 + pK3)
L’étude de la fonction (AH2±) = f (H+) permet de remarquer que le point isoélectrique est
défini comme le pH pour lequel (AH2±) est maximum.
Détermination de la mobilité ionique :
On appelle mobilité d'un ion, la vitesse limite atteinte par cet ion dans un champ électrique
unitaire.
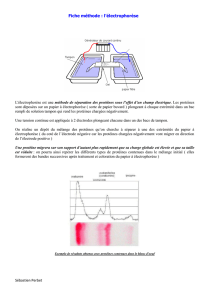
Si on établit une différence de potentiel entre les extrêmités d'une bande de papier imprégnée
par un électrolyte convenable, une goutte de solution contenant l'espèce ionique à étudier étant
déposée sur la bande, les constituants ioniques se déplacent sous l'action du champ électrique
avec leurs vitesses propres. Les déplacements peuvent être suivis et mesurés après révélation
par un procédé approprié.

Cnam Paris, Electrochimie Industrielle - Travaux pratiques B1, N°5
4
Cependant, les vitesses expérimentales déterminées à partir de la mesure du déplacement des
ions ne correspondent pas à un déplacement vrai dû uniquement au champ électrique. En effet,
le passage du courant dans la bande d'électrophorèse provoque par effet Joule un échauffement
du liquide qui se traduit par une évaporation de l'électrolyte d'imprégnation. Or, les deux
extrêmités de la bande plongeant dans des bacs contenant cet électrolyte, l'eau qui s'évapore est
donc continuellement remplacée par du liquide frais provenant des bacs à électrode. Ceci
provoque un courant hydrodynamique dont les effets viennent se superposer à ceux du champ
électrique.
+ -
sens de migration des cations
axe
flux hydrodynamique
évaporation
On voit que la vitesse d'entraînement due au flux hydrodynamique peut être soit positive, soit
négative, suivant la région de la feuille où la solution à étudier a été déposée. Ainsi, le
déplacement des ions dépendra de leur position de départ.
De plus, à ce phénomène d'évaporation, vient s'ajouter le phénomène
d'électroosmose.Toutefois, celui-ci est constant tout au long de la bande si le champ est bien
uniforme et, pour des temps relativement courts, il est très peu important. Donc, en pratique,
nous considérons les vitesses d'entraînement électroosmotique comme négligeables.
Dans ces conditions, la vitesse expérimentale de déplacement Vexp peut être décomposée en
deux termes:
• la vitesse vraie: Vvraie
• la vitesse due aux flux hydrodynamique: Vhydro
Vexp = Vvraie + Vhydro
Pour obtenir la vitesse vraie, il sera nécessaire de faire la correction due au flux
hydrodynamique.
Dans certains cas, on arrive à avoir la vitesse vraie directement par expérience. Ceci est réalisé
lorsque le point de départ et le point d'arrivée des ions étudiés sont symétriques par rapport au

Cnam Paris, Electrochimie Industrielle - Travaux pratiques B1, N°5
5
centre de la bande d'électrophorèse. Dans ce cas, les effets du flux hydrodynamique sont égaux
et de signe contraire de part et d'autre de l'axe, par conséquent l'effet total est nul.
• Détermination de la vitersse vraie :
Il est possible de déterminer la vitesse vraie par une série de mesures que nous allons décrire.
axe de la feuille
A1
A2
A3
A4
A5 A6
A7
A8
B1
B2
B3
B4
B5
B6
B7
B8
(0)
Considérons une feuille de papier sur laquelle est faite l'électrophorèse. On appelle YY' l'axe de
la feuille perpendiculaire du champ électrique. Soient A le point de départ de l'ion étudié, B le
point d'arrivée de cet ion après passage du courant.
On réalise une série de points A situés à des distances variables de YY', ce qui donne une série
de points B. Pour chaque ensemble A et B, considérons la quantité algébrique y = OA + OB.
Si on appelle x la distance de A à YY', on a:
OA = x, OB = OA + AB = x + D
D étant le déplacement de l'ion, variable avec sa position de départ. On a donc:
y = 2x + D
Nous avons vu plus haut que l'on obtenait la valeur du déplacement vrai pour un point de départ
symétrique au point d'arrivée par rapport à YY',c'est-à-dire, en supposant l'axe des x orienté
dans le sens du déplacement:
x = - D/2
Dans ces conditions, la quantité y est nulle. Ainsi, on voit qu'en représentant la variation de y =
f(x), on obtient pour y = 0, une valeur de x qui est égale au demi-déplacement vrai changé de
signe.