Exercices d`océanographie, niveau L3 Version mise `a jour

Exercices d’oc´ eanographie, niveau L3
Version mise ` a jour le 3 f´ evrier 2015
Table des mati` eres
1 Manipulation des ´ equations de base 2
2 G´ eostrophie et processus d’Ekman 3
3 Mod` eles de Sverdrup et de Stommel 3
4 Caract´ eristiques physiques de l’eau de mer 4
5 Masses d’eau 5
6 Echantillon de contrˆ oles continus et examens pass´ es 8
6.1 Examen2008 ...................................... 8
6.2 Contrˆ olecontinu2009 ................................. 9
6.3 Examen2009 ...................................... 10
6.4 Contrˆ olecontinu2010 ................................. 12
6.5 Examen2010 ...................................... 16
6.6 Contrˆ olecontinu2013 ................................. 18
6.7 Examen2013 ...................................... 19
6.8 Contrˆ olecontinu2014 ................................. 21
6.9 Examen2014 ...................................... 22
1

1 Manipulation des ´ equations de base
Exercice 1 : Conservation de la masse
1. Une couche d’eau incompressible d’´ epaisseur constante, sans mouvements verticaux, poss` ede une
vitesse moyenne zonale :
U=U0(1 −x/Lx) sin(2πy/Ly).
Peut-on calculer la vitesse m´ eridienne ?
2. Une couche d’eau se d´ eplace zonalement vers un talus de pente constante (voir figure 1). Le d´ ebit
de l’´ ecoulement est constant et la vitesse verticale ` a la surface est nulle. Calculer la vitesse verticale
du fond de la couche de 2 fac¸ons : en ´ ecrivant la vitesse d’une parcelle d’eau au fond de la couche,
puis en utilisant la loi de conservation de la masse.
Figure 1 – Courant passant sur un talus.
Exercice 2 : La tache rouge de Jupiter
La tache rouge de Jupiter se situe autour de 22◦S, s’´ etend sur 12◦en latitude et 25◦en longitude.
Elle pr´ esente des vents de 110 m/s, et d´ erive zonalement ` a une vitesse de 3 m/s. Le rayon de Jupiter
est 71400 km et son jour dure 9.9 heures. La tache est-elle influenc´ ee par la rotation jovienne ?
Exercice 3 : Equilibre hydrostatique
L’eau de mer a une masse volumique de 1028 kg.m−3. Calculer la pression ` a 10 m de profondeur,
puis ` a 10000 m (fosse des Mariannes). Mˆ eme question lorsque la masse volumique de l’eau de mer
varie lin´ eairement de 1023 ` a la surface ` a 1028 ` a 2000 m, puis reste ` a 1028 apr` es.
Exercice 4 : Oscillation inertielle
Dans les hautes latitudes nord, une bou´ ee d´ erivante est port´ ee par le courant de surface. Du vent
souffle puis s’arrˆ ete, si bien que l’´ evolution temporelle du courant est uniquement d´ etermin´ ee par la
2

force de Coriolis. Caract´ eriser ce courant.
Exercice 5 : Oscillation inertielle et mar´ ees
D´ eterminer la latitude ` a laquelle les oscillations inertielles peuvent entrer en r´ esonance avec les
mar´ ees diurnes et semi-diurnes.
2 G´ eostrophie et processus d’Ekman
Exercice 6 : G´ eostrophie
Dans la Manche (50 ◦N), repr´ esent´ ee comme un canal rectangulaire de 200 km de large et orient´ e
d’Ouest en Est, une mar´ ee g´ en` ere un courant zonal de 1 m/s.
1. En consid´ erant cet ´ ecoulement g´ eostrophique, calculer la diff´ erence de pression entre un point de
la cˆ ote anglaise et un autre point, de mˆ eme profondeur, de la cˆ ote franc¸aise.
2. En consid´ erant l’´ equilibre hydrostatique, calculer la diff´ erence de niveau de l’eau entre les deux
cˆ otes.
Exercice 7 : Processus d’Ekman
A 45◦N, le vent souffle du Sud-Ouest ` a 10 m/s au-dessus de l’eau. D´ eterminer le transport moyen
dans la couche d’Ekman. On prendra 1.2 10−3pour le coefficient de traˆ ın´ ee et 1.29 kg.m−3comme
masse volumique de l’air. Calculer le courant moyen dans la couche d’Ekman.
Exercice 8 : Effet beta
1. Rappeler ce qu’est l’effet beta et de quelle(s) loi(s) il d´ ecoule.
2. Une colonne d’eau se d´ eplac¸ant d’Ouest en Est avec une vitesse U constante aborde une pente
constante d’angle αavec l’horizontale (figure 1). La mer reste plane (la vitesse verticale de surface est
nulle). Calculer la vitesse m´ eridienne induite.
3. Tracer, qualitativement et en vue de dessus, la trajectoire d’une colonne d’eau qui croise une dor-
sale, d’Ouest en Est dans l’h´ emisph` ere Sud.
3 Mod` eles de Sverdrup et de Stommel
Exercice 9 :
On mod´ elise le courant circumpolaire antarctique comme un canal zonal dont les fronti` eres sont
situ´ ees ` a 40 et 50◦S, et referm´ e sur lui-mˆ eme (il fait le tour du globe). Un vent zonal souffle d’Ouest
en Est. On consid` ere que les fronti` eres nord et sud empˆ echent le d´ eveloppement d’un courant m´ eridien.
3

1. D´ ecrire qualitativement l’´ equilibre qui va s’instaurer.
2. Le mod` ele de Sverdrup peut-il aider ` a l’´ etude ?
3. En se basant sur le mod` ele de Stommel, d´ eterminer le courant zonal et le gradient de pression en
jeu.
4. La d´ enivellation observ´ ee par satellite est d’environ 1,5 m entre 40 et 50◦S. D´ eterminer num´ eriquement
le courant zonal.
4 Caract´ eristiques physiques de l’eau de mer
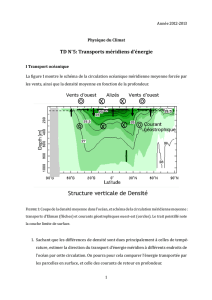
Exercice 10 :
1. Restituer sa l´ egende ` a la figure 2 et expliquer la diff´ erence entre les 2 sections.
2. La salinit´ e est homog` ene. Une parcelle d’eau entre dans la section de droite le long de l’isoligne
1.1. Comment va-t-elle ´ evoluer apr` es le passage de la crˆ ete des Mariannes ?
Figure 2–L´ egende ` a d´ eterminer !
Exercice 11 :
Discuter la stabilit´ e des profils de la figure 3.
Exercice 12 :
Discuter la stabilit´ e et la possibilit´ e d’existence des colonnes d’eau dont les profils de temp´ erature
potentielle sont pr´ esent´ es sur la figure 4. Eventuellement, d´ eterminer les lieux g´ eographiques de telles
colonnes d’eau.
Exercice 13 :
Une mer de 1000 m de profondeur, constitu´ ee d’eau ` a 20◦C et ` a 37 g/kg de sel, cˆ otoie un lac ` a
15◦C de 1000 m de profondeur ´ egalement. Au cours d’un s´ eisme, un d´ etroit s’ouvre sur une profon-
4

!
"
#$$$
#%$%
!&'()*+#$&,,!"#$%&'(!"#))&)%&*+
-
!
"
#$$$
#%$%
!&'()*+#$&#%&,,!"#))&*+"#)%&*,
.
!
"
#$$$
#%$%
!&'()*+#$&#%&,,!"#))&*+"#)%&*-
/
!
"
#$$$
#%$%
!&'()*+#$&,,!"#$%&'(!"#))&*+"#)%&*-
!
!
"
#$$$
#%
!&'()*+0&,()*+1&2((()*+#$&,,!"#$.&'(!"#
$%&'*!"#))&*+#/01234#5678.911:;69;<
3
0
1
Figure 3 – Profils de temp´ erature et de salinit´ e.
deur de 100 m, entre les deux. Que se passe-t-il ?
Exercice 14 :
Des mesures de temp´ erature et de salinit´ e ont ´ et´ e effectu´ ees le long d’un profil vertical dans l’atlan-
tique ´ equatorial. Les r´ esultats de ces mesures sont report´ es dans la table 1. Comment proc´ eder pour
d´ eterminer la stabilit´ e d’un profil vertical ? Le profil ci-dessus est-il stable ? Quelles masses d’eau
reconnait-on ?
5 Masses d’eau
Exercice 15 : Caract´ erisation d’une masse d’eau
La mer de Weddell (Antarctique) est l’un des principaux lieux de formation d’eau profonde An-
5