Mémoire V16 - Olympiades de Physique

1
Académie de Créteil

2
Table des matières
Résumé ............................................................................................................................................................................. 3
Introduction...................................................................................................................................................................... 3
I. Expérience n°1 : Les tubes paresseux ...................................................................................................................... 3
II. Mise en évidence du lien entre électricité et magnétisme .................................................................................... 4
A. Expérience n°2 : Œrsted ....................................................................................................................................... 4
B. Expérience n°3 ...................................................................................................................................................... 4
III. Force de Lorentz et force de Laplace ................................................................................................................... 5
A. La force de Lorentz : ............................................................................................................................................. 5
B. Expérience n°4 : le rail de Laplace : ..................................................................................................................... 5
C. Force de Laplace : ................................................................................................................................................. 6
IV. Induction............................................................................................................................................................... 6
A. Flux magnétique ................................................................................................................................................... 6
B. Mise en évidence du phénomène d’induction .................................................................................................... 6
C. Loi de Lenz-Faraday : ............................................................................................................................................ 7
V. La maquette ............................................................................................................................................................. 7
A. Projet initial .......................................................................................................................................................... 7
B. Les solénoïdes ...................................................................................................................................................... 7
C. Le choix du disque ................................................................................................................................................ 8
D. La réalisation de la maquette ............................................................................................................................ 10
A. Choix du système ............................................................................................................................................... 11
B. Repères et notations : ........................................................................................................................................ 11
C. Résolution de l’équation différentielle et expression de la vitesse ................................................................. 15
E. Valeurs des paramètres expérimentaux ........................................................................................................... 16
F. Exploitation des mesures ................................................................................................................................... 17
Remerciements .............................................................................................................................................................. 20
Bibliographie .................................................................................................................................................................. 20

3
Résumé
Est-il possible de freiner une cabine d’ascenseur sans contact ? Lors d’une promenade dans la forêt de l’électromagnétisme,
en bifurquant vers le lien entre électricité et magnétisme, sans oublier d’admirer les forces de Laplace et de Lorentz, nous
survolerons les phénomènes d’induction pour parvenir à la clairière des courants de Foucault. À travers la maquette d’ascenseur
freinée par des aimants que nous avons réalisé, nous vous montrerons qu’un frein n’est pas souvent ce qu’il semble être et que
parfois, la réalité dépasse la fiction ! Enfin, vous ferez un tour dans notre ascenseur pour regagner la terre ferme et vous verrez que
plus longue sera la chute…
Introduction
Nous avons tous déjà vu au moins une fois dans notre enfance un film dans lequel un superhéros sauve la vie de pauvres
civils innocents en arrêtant un ascenseur en pleine chute ou bien un train dont la vitesse était incontrôlable ! Et ce, grâce à la seule
force de sa pensée et de ses muscles !
De sa pensée et de ses muscles, ou bien des ondes qui s’en dégageaient ? Pouvons-nous percer le secret des dessins animés qui ont
construit notre enfance et ainsi imaginer un moyen permettant de freiner un système en mouvement sans aucun contact ? La
physique et l’électromagnétisme nous répondent que oui !
Au-delà de notre goût pour la science-fiction, on peut même imaginer que ce mécanisme puisse diminuer l’usure des
matériaux, ce qui permettrait de faire de grandes économies.
C’est par cette motivation que nous avons décidé de nous intéresser à ces phénomènes électromagnétiques qui pourraient
expliquer, dans le but de réaliser nous-même une maquette d’ascenseur fonctionnant sur un système de « freinage magnétique »
par courants de Foucault.
Dans un premier temps, nous avons effectué diverses recherches et expériences afin de comprendre les mécanismes de ce
freinage, puis nous nous sommes lancés dans le cœur de notre projet, à savoir la construction d’un ascenseur à échelle réduite
freiné par courants de Foucault.
I. Expérience n°1 : Les tubes paresseux
Soit un aimant, de masse  que l’on fait chuter dans un cylindre en
cuivre, de longueur. On cherche à déterminer la durée nécessaire à
l’aimant pour parcourir le cylindre.
On se place dans le référentiel du laboratoire qui est un référentiel
terrestre, supposé galiléen, avec un vecteur unitaire  orienté vers le haut.
On considère que l’aimant est en chute libre dans le cylindre en cuivre
afin de pouvoir négliger les frottements de l’air. La masse du système étant
constante, la deuxième loi de Newton peut s’écrire :
Or, l’aimant est en chute libre. Par définition, il n’est soumis qu’à son poids :
On projette cette relation sur les différents axes du repère d’étude :
!"
Par intégration, on a :
# $#
%
&
# %
'
# !()%
*
"
Où %
&
, %
&
et %
*
sont des constantes d’intégration que l’on détermine à l’aide des
conditions initiales. L’objet étant lâché sans vitesse initiale, à (+, #
,
et : #
,
$#
,
%
&
#
,
%
'
#
,
%
*
"
z
-
y
x
Fig. 1

4
Les coordonnées du vecteur vitesse sont donc : #
.#
#
# !("
Sachant que le vecteur vitesse # /# # # 0 est la dérivée du vecteur position 12 34567, par intégration, on obtient :
12 84%
9
5%
:
6!;
<(
'
)%
=
"
Où %
9
, %
:
et %
=
sont des constantes d’intégration que l’on détermine à l’aide des conditions initiales. À (+, l’objet est lâché
d’une hauteur initiale  :
12
,
84
,
%
9
5
,
%
:
6
,
!;
<
'
)%
=
">.%
9
%
:
%
=
"
Selon, l’axe vertical, on obtient l’équation horaire suivant :
6!;
<(?)
On s’interroge maintenant sur la durée nécessaire au système pour parcourir toute la longueur du tube c’est-à-dire la durée pour
laquelle il atteint 6
6 !;
<(
'
) !;
<(
'
! (
'
< (?<
 (@<
 (@<
 (AB+
Donc, en faisant chuter l’aimant dans notre cylindre en cuivre, l’aimant devrait ressortir du tube en 0,45 s. Or, en faisant cette
expérience, on constate que l’aimant parcourt le cylindre en cuivre en 10 s. Soit, près de 22 fois le temps estimé théoriquement ! À
quoi est due cette différence ?
À notre échelle les frottements de l’air sont négligeables et ne peuvent donc pas être responsables d’une telle différence
entre la théorie et notre expérience. Une autre force doit donc provoquer ce phénomène. Afin de déterminer sa nature, nous avons
réalisé la même expérience avec d’autres objets non-aimantés, et le résultat obtenu était proche du résultat théorique. Nous avons
alors conclu que la force qui freinait l’aimant était liée à sa nature.
Nos recherches nous ont alors menés aux courants de Foucault. Avant de nous intéresser plus en détail à ces courants de
Foucault, nous nous sommes donc d’abord intéressés au lien entre l’électricité et le magnétisme.
II. Mise en évidence du lien entre électricité et magnétisme
A. Expérience n°2 : Œrsted
L’expérience historique d’Oersted (1820) consiste à faire passer un
courant électrique sans un fil situé à proximité de l’aiguillé aimanté
d’une boussole.
Naturellement, l’aiguille est orientée selon le champ magnétique de la
Terre, C
DEE
.
Lorsqu’un courant circule dans le fil, on observe alors que l’aiguille est
déviée. Comme l’aiguille ne peut être déviée que par un champ
magnétique, on peut en déduire que le courant électrique crée un
champ magnétique. Réciproquement, on peut se demander si un champ magnétique peut induire un courant électrique.
I
N
S
N
S
I = 0
Fig. 3a
Fig. 3b
Fig. 2
Fig.
2

5
B. Expérience n°3
Afin de savoir si un champ magnétique peut induire un courant électrique, on
relie une bobine à un ampèremètre, sans aucun générateur. Lorsque l’aimant est
immobile, aucun courant ne circule. A l’inverse, lorsque l’on déplace l’aimant à
proximité de la bobine, l’ampèremètre affiche une valeur d’intensité, ce qui montre
qu’un courant circule dans la bobine. On peut donc en déduire qu’un champ magnétique
créé par un aimant statique n’induit pas de courant électrique, mais que c’est le
mouvement de l’aimant qui a été à l’origine de l’apparition d’un courant.
Avant de faire appel à la théorie pour expliquer ce phénomène, nous avons d’abord voulu vérifier que ce lien étroit entre
électricité et magnétisme pouvait bien modifier le mouvement d’un objet. Plus précisément, dans le cas de l’expérience du tube
paresseux, nous nous sommes demandé si un courant électrique qui serait induit par le champ magnétique de l’aimant pouvait être
suffisant pour freiner l’aimant.
Nous avons alors découvert les forces de Lorentz et de Laplace qui, à travers l’expérience du rail de Laplace, pouvaient nous aider à
expliquer le phénomène en jeu dans l’expérience du tube paresseux.
III. Force de Lorentz et force de Laplace
A. La force de Lorentz :
En électromagnétisme, on s’intéresse principalement au mouvement d’une charge Fqui, dans des champs électrique et
magnétique caractérisés respectivement par les vecteurs champs G et C , se déplace à une vitesse # . Cette charge subit ainsi la
force suivante :  F/G )# HC 0
On peut alors distinguer deux forces différentes dans cette formule :
• Force électrique donnée par la loi de Coulomb :  FG
• Force magnétique : 
IJK
F# HC
Remarques :
- Lorsque la particule est immobile /# 0, la force de Lorentz est nulle, et la charge est alors soumise uniquement à la
force électrique.
- Par cette relation, on observe le lien entre électricité et magnétisme que nous avons mis en évidence dans les expériences
(2) et (3).
Pour en revenir à la force de Lorentz, cette dernière est une force électromagnétique élémentaire. En effet, c’est la force que subit
une particule chargée dans un champ magnétique et/ou électrique et elle est responsable de la majorité des interactions électriques
et magnétiques observées.
Cette force représentée par un vecteur a les caractéristiques suivantes :
 Point d’application : particule chargée du système étudié.
 Direction : perpendiculaire au plan formé par le conducteur et au champ magnétique B.
 Sens : déterminé par la règle de la main droite.
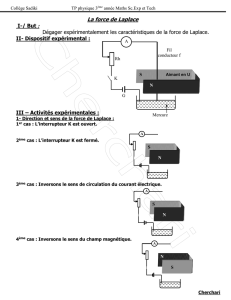
B. Expérience n°4 : le rail de Laplace :
On place un conducteur mobile sur deux rails horizontaux connectés à un
générateur et on pose un aimant permanent en U entre les deux tiges. Puis, on place la
tige conductrice mobile entre les rails de telle façon qu’il se trouve dans le champ
magnétique de l’aimant permanent en U. On allume ensuite le générateur afin qu’un
courant circule dans les rails.
On observe alors que le conducteur mobile roule d’un côté ou de l’autre selon
le sens du courant. À l’inverse, lorsqu’aucun courant ne circule, ou lorsque l’aimant est
retiré du dispositif, la tige métallique ne se met pas en mouvement. On en déduit ainsi
que le mouvement de la tige est dû à une force provoquée à la fois par la présence du champ magnétique et du courant électrique :
cette force ressemble donc à la force de Lorentz. Pourtant, nous avons vu que la force de Lorentz ne s’applique qu’à l’échelle
microscopique. La force impliquée dans l’expérience du rail n’est donc pas la force de Lorentz mais celle de Laplace.
Fig. 4
Fig. 5