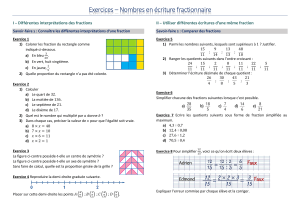
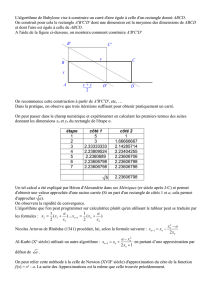
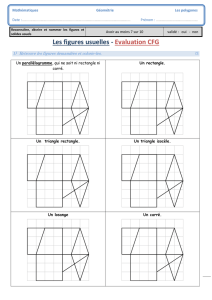
Structure des nombres réels Partie I

1842
x x = [x]+{x}[x]
x{x}[0,1[
x x
x= [x]{x}= 0 0 <{x}<1x1= 1/{x}
x1x x1= [x1] + {x1}
[x1]≥1x1

x= [x] + 1
[x1],
x1x2= 1/{x1}
x= [x] + 1
x1
= [x] + 1
[x1] + 1
x2
= [x] + 1
[x1] + 1
[x2] + 1
. . .
.
x= 4,16
x=√2
e
π
1x x > 0
1x
1{x}{x}
4,16
√2

x
p/q p ∈Zq∈Z∗
x=p/q
q
p q
√2
√2
1 + √2 = 2 + 1
1 + √2.
√2
a+b b √2 = a/b
b b a −b
a+b
b=b a−b.

√2√2 = a/b b
a
b < a < 2b
√2 = 2b−a
a−b.
0< a −b < b
Φ
Φ = 1 + √5
2.
√2
Φ = 1 + 1
Φ.

e
e
e
e−1
2.
e−2.
e