nombres réels - Laurent Garcin

©Laurent Garcin MPSI Lycée Jean-Baptiste Corot
NOMBRES RÉELS
1 Approximations d’un réel
1.1 Ensembles de nombres
Notation 1.1
IOn note Rl’ensemble des nombres réels.
IOn note Ql’ensemble des nombres rationnels i.e. l’ensemble des nombres de la forme p
qavec (p, q)∈
Z×N∗. Un nombre réel non rationnel est dit irrationnel.
IOn note Dl’ensemble des nombres décimaux i.e. l’ensemble des nombres de la forme a
10navec (a, n)∈
Z×N.
IOn note Zl’ensemble des entiers relatifs.
IOn note Nl’ensemble des entiers naturels.
Remarque. On a N⊂Z⊂D⊂Q⊂R.
Exemple 1.1
√2est irrationnel.
1.2 Partie entière
Le théorème suivant découle de la construction des entiers.
Théorème 1.1 Propriété fondamentale des entiers
Toute partie non vide et majorée (resp. minorée) de Zadmet un plus grand élément (resp. un plus petit
élément).
Ce théorème légitime la définition suivante.
Définition 1.1 Partie entière d’un réel
Soit x∈R. On appelle partie entière de x, notée bxc, le plus grand entier relatif inférieur ou égal à x.
Proposition 1.1 Caractérisation de la partie entière
Soit (x, k)∈R×Z.
k=bxc⇐⇒ x−1<k6x⇐⇒ k6x<k+1
Remarque. Il pourra être utile dans les exercices de remarquer que si net psont des entiers
n<p ⇐⇒ n6p−1⇐⇒ n+16p
http://laurentb.garcin.free.fr 1

©Laurent Garcin MPSI Lycée Jean-Baptiste Corot
Remarque. On appelle partie fractionnaire de xle réel noté {x}=x−bxc. On a donc {x}∈[0, 1[.
Proposition 1.2 Propriétés de la partie entière
(i) La partie entière est une application croissante.
(ii) ∀x∈R,x=bxc⇐⇒ x∈Z.
(iii) ∀(x, n)∈R×Z,bx+nc=bxc+n.
Attention ! En général, bx+yc 6=bxc+bycet bnxc 6=nbxcmême si nest entier.
Attention ! La partie entière est croissante i.e.
∀(x, y)∈R2, x 6y=⇒bxc6byc
Mais la partie entière n’est pas strictement croissante. Par exemple, 0 < 1
2mais b0c=1 2.
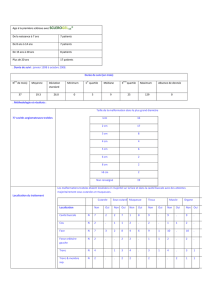
−3−2−1 1 2 3
−3
−2
−1
1
2
3
ILa partie entière est croissante.
ILa partie entière est constante par morceaux.
ILa partie entière présente des discontinuité
en les entiers relatifs.
ILa partie entière est continue en tout réel non
entier.
ILa partie entière est continue à gauche et non
à droite en tout entier.
Graphe de la partie entière
Remarque. Pour x∈R, le plus petit entier relatif supérieur ou égal à xse note dxe. Si k∈Z, alors
k=dxe⇐⇒ x6k<x+1⇐⇒ k−1 < x 6k
On a en fait dxe= −b−xc.
1.3 Approximations décimales
Définition 1.2
Soient x∈Ret n∈N. On pose Dn=a
10n, a ∈Z.
IOn appelle valeur décimale approchée de xà10−nprès par défaut l’unique décimal αn∈Dn
tel que α6x<α+10−n.
IOn appelle valeur décimale approchée de xà10−nprès par excès l’unique décimal βn∈Dntel
que β−10−n< x 6β.
http://laurentb.garcin.free.fr 2

©Laurent Garcin MPSI Lycée Jean-Baptiste Corot
Exemple 1.2
3, 1415 est une valeur décimale approchée de πà10−4près par défaut.
3, 1416 est une valeur décimale approchée de πà10−4près par excès.
Remarque. On peut exprimer αnet βn. En fait,
αn=b10nxc
10nβn=d10nxe 10n
Si x∈D, alors αn=βn=x.
Sinon, βn=αn+10−n.
Remarque. αest le nombre décimal dont les décimales (chiffres après la virgule) sont les npremières décimales
de x.
1.4 Densité dans R
Définition 1.3 Densité
Soit Aune partie de R. On dit que Aest dense dans Rsi tout intervalle ouvert non vide de Rcontient au
moins un élément de A.
Proposition 1.3 Caractérisation « epsilonesque » de la densité
Soit Aune partie de R.Aest dense dans Rsi et seulement si
∀x∈R,∀ε > 0, ]x−ε, x +ε[∩A 6=∅
Proposition 1.4 Caractérisation séquentielle de la densité
Soit Aune partie de R.Aest dense dans Rsi et seulement si pour tout x∈R, il existe une suite (xn)
d’éléments de Ade limite x.
Proposition 1.5 Densité de D,Qet R\Qdans R
D,Qet R\Qsont denses dans R.
2 Relation d’ordre sur R
2.1 Majoration et minoration
Définition 2.1 Parties majorées, minorées, bornées
Soit Aune partie de R.
IOn dit que Aest majorée s’il existe M∈Rtel que x6Mpour tout x∈ A. Dans ce cas, on dit que
Mest un majorant de A.
IOn dit que Aest minorée s’il existe m∈Rtel que x>mpour tout x∈ A. Dans ce cas, on dit que
mest un minorant de A.
IOn dit que Aest bornée si elle est majorée et minorée.
http://laurentb.garcin.free.fr 3

©Laurent Garcin MPSI Lycée Jean-Baptiste Corot
Proposition 2.1
Soit Aune partie de R.Aest bornée si et seulement si il existe K∈Rtel que |x|6Kpour tout x∈ A.
2.2 Maxima et minima
Définition 2.2 Maximum et minimum
Soit Aune partie de R.
IOn dit que Mest le maximum ou le plus grand élément de Asi M∈ A et Mest un majorant de
A. On note alors m=min A.
IOn dit que mest le minimum ou le plus petit élément de Asi m∈ A et mest un minorant de A.
On note alors M=max A.
Exemple 2.1
−1et 1sont respectivement le minimum et le maximum de l’intervalle [−1, 1].
Attention ! Une partie de Rn’admet pas forcément de maximum ou de minimum. Par exemple, ] − 1, 1[
n’admet ni minimum ni maximum. En particulier, −1et 1ne sont pas le minimum et le maximum de ] − 1, 1[
puisqu’ils n’appartiennent pas à cet intervalle.
2.3 Bornes inférieures et supérieures
Définition 2.3 Borne inférieure et supérieure
Soit Aune partie de R.
IOn appelle borne supérieure de Ale minimum de l’ensemble des majorants de A,s’il existe. Dans
ce cas, on le note sup A.
IOn appelle borne inférieure de Ale maximum de l’ensemble des minorants de A,s’il existe. Dans
ce cas, on le note inf A.
Rien ne garantit a priori l’existence d’une borne inférieure ou supérieure. On a néanmoins le théorème suivant.
Théorème 2.1 Propriété de la borne supérieure
Toute partie non vide et majorée (resp. minorée) de Rpossède une borne supérieure (resp. inférieure).
Remarque. Ce théorème est admis car il découle directement de la construction de Rqui est hors programme.
Pour votre culture, le corps des réels Rest construit à partir des corps des rationnels Qde façon à ce qu’il possède
justement cette propriété de la borne supérieure.
Proposition 2.2
Soit Aune partie de R.
ISi M=max A, alors M=sup A.
ISi m=min A, alors m=inf A.
http://laurentb.garcin.free.fr 4

©Laurent Garcin MPSI Lycée Jean-Baptiste Corot
Attention ! Les réciproques sont fausses ! Une partie de Rpeut posséder une borne supérieure (resp. infé-
rieure) sans posséder de maximum (resp. minimum).
Exemple 2.2
Les bornes inférieures et supérieures de [−2, 1[sont −2et 1. De plus, −2est le plus petit élément de Amais
[−2, 1[ne possède pas de plus grand élément.
Les propositions suivantes permettent de déterminer des bornes supérieures et inférieures en pratique.
Proposition 2.3 Caractérisation « epsilonesque » des bornes inférieures et supérieures
Soient Aune partie de Ret c∈R.
c=inf Asi et seulement si cest un minorant de Aet si pour tout ε > 0, il existe a∈ A tel que
c+ε>a.
c=sup Asi et seulement si cest un majorant de Aet si pour tout ε > 0, il existe a∈ A tel que
c−ε<a
Proposition 2.4 Caractérisation séquentielle des bornes inférieures ou supérieures
Soient Aune partie de Ret c∈R.
Ic=inf Asi et seulement si cest un minorant de Aet s’il existe une suite (an)d’éléments de Ade
limite c.
Ic=sup Asi et seulement si cest un majorant de Aet s’il existe une suite (an)d’éléments de Ade
limite c.
Exercice 2.1
Déterminer les bornes supérieure et inférieure de 3
2p−1 3q,(p, q)∈N2.
Méthode Passage à la borne supérieure/inférieure
ISi ∀x∈ A, x 6M, alors sup A6M.
ISi ∀x∈ A, x >M, alors inf A>M.
Attention ! Le passage à la borne supérieure/inférieure ne conserve que les inégalités larges, exactement
comme le passage à la limite.
Exercice 2.2
Soient Aet Bdeux parties non vides de R. On définit A+B={x+y|(x, y)∈ A × B}.
1. On suppose Aet Bmajorées. Montrer que sup A+B=sup A+sup B.
2. On suppose Aet Bminorées. Montrer que inf A+B=inf A+inf B.
http://laurentb.garcin.free.fr 5