I. Mouvement d`un point

Mouvement d'un solide
I. Mouvement d'un point
1. Relativité du mouvement:
Définition
On appelle référentiel un objet par rapport auquel le physicien étudie le
mouvement. Tout mouvement est relatif au référentiel utilisé (voir cours de
seconde).
2. Repère d'espace:
Pour repérer la position d'un mobile, il est nécessaire d'associer un repère au
référentiel.
Définition
On appelle repère le système de
repérage dans l'espace associé au
référentiel.
3.Date:
Un événement est repéré par sa date. Une durée est l'intervalle de temps
séparant deux dates.
II. Vitesse d'un point
1. Vitesse moyenne:
Définition

On appelle vitesse moyenne d'un solide ponctuel le quotient de la distance
parcourue par le solide par le temps mis pour la parcourir.
Mouvement rectiligne
Mouvement curviligne
2. Vitesse instantanée
Définition
On appelle vitesse instantanée d'un solide ponctuel à
la date t la vitesse moyenne du solide pendant une
brève durée autour de la date t.
Remarques
 La vitesse du mobile dépend du référentiel utilisé.
 La vitesse instantanée est la valeur indiquée par le tachymètre (indicateur
de vitesse) d'un véhicule.
 Le mouvement est dit uniforme si la valeur de la vitesse instantanée reste
constante.
 Le mouvement est dit accéléré si la valeur de la vitesse instantanée
augmente au cours du temps.
 Le mouvement est dit décéléré si la valeur de la vitesse instantanée
diminue au cours du temps.
3. Vecteur vitesse
Définition
A un instant de date t, le mouvement d'un mobile est déterminé par:
 La position du mobile.
 Le vecteur vitesse du mobile caractérisé par:
o sa direction: la tangente à la trajectoire.
o son sens :celui du mouvement.
o sa valeur: la vitesse instantanée du mobile.
III. Mouvement d'un solide indéformable

1. Définition:
On appelle solide indéformable un objet matériel dont la
distance entre deux points quelconques ne varie pas au cours
du temps.
2. Trajectoires:
Définition:
On appelle trajectoire d'un mobile l'ensembles des positions successives de ce
mobile au cours du temps.
 Le mouvement d'un objet est dit curviligne si sa trajectoire est une
courbe.
 Le mouvement d'un objet est dit rectiligne si sa trajectoire est une droite.
 Le mouvement d'un objet est dit circulaire si sa trajectoire est un cercle.
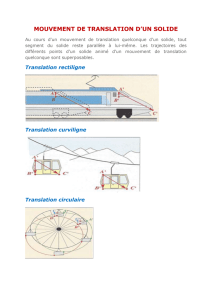
3. Mouvement de translation:
Définition:
Un solide possède un mouvement de translation si tout segment du solide reste
parallèle à lui même au cours du mouvement.
4. Trajectoires dans un mouvement de translation
Translation rectiligne: Tout segment du solide se déplace en restant parallèle à
lui même et le mouvement de chaque point est rectiligne.
Translation curviligne: Tout
segment du solide se déplace en
restant parallèle à lui même et le
mouvement de chaque point est
curviligne.

Translation circulaire: Tout segment du solide se déplace en restant parallèle à
lui même et le mouvement de chaque point est un cercle.
5. Solide en rotation autour d'un axe fixe:
a. Définition
Un solide possède un mouvement de rotation autour d'un axe fixe si le
mouvement de chacun de ses points est un
cercle centré sur l'axe de rotation.
b. Vitesse angulaire
Définition: On appelle vitesse angulaire
moyenne le quotient de l'angle dont a tourné
le solide par le temps mis pour effectuer cette
rotation.
w
m
=
q2 - q1
t2 - t1
avec
wm en en rad .s-1
q2 et q1 en radians
(rad)
t2 et t1 en secondes
(s)
Définition: On appelle vitesse angulaire instantanée d'un solide à la date t la
vitesse angulaire moyenne du solide pendant une brève durée autour de la date
t.
w
=
q2 - q1
t2 - t1
avec
t2 t1
c. Relation entre V et w

Vm
=
M1M2
t2 - t1
=>
Vm
=
OM2 - OM1
t2 - t1
=>
Vm
=
R.q2 - R.q1
t2 - t1
=>
Vm = R. wm
La relation reste vraie si t2 t1.
V = R . w
V: vitesse linéaire en m.s-1.
R: rayon de la trajectoire en m.
w: vitesse angulaire en rad.s-1
IV. Centre d'inertie
1. Définition:
On appelle centre d'inertie d'un solide en
mouvement le point de ce solide dont le
mouvement est le plus simple. On le note G.
Exemple: Mobile muni d'un éclateur central
A et d'un éclateur périphérique B.
Lorsque le mobile est en mouvement, le
point A décrit une trajectoire plus simple
(rectiligne) que celle des autres points. Le
point A est le centre d'inertie du mobile.
2. Solides de formes géométriques simples:
Dans le cas où le solide est homogène et où il présente un centre de symétrie,
le centre d'inertie est confondu avec ce point.