DS 4 - TS - complexes

DS 4 – Terminale S – Nombres Complexes
Dans tous les exercices, le plan complexe sera muni du repère orthonormé (O, U, V).
EXERCICE 1 :
1) Ecrire les nombres complexes suivants sous forme exponentielle.
z
1
= -2 +2 i 3 z
2
= 3 + 3i z
3
= z
1
z
2
z
4
= (z
1
)
8
. (z
2
)
3
2) Ecrire z
3
sous forme algébrique.
3) En déduire les valeurs exactes de cos ( 5π
12 ) et sin ( 5π 12 )
4) Placer précisément les points M,N,P d’affixes respectives z
1
, z
2
, z
3
. Expliquer la construction
EXERCICE 2 : (les parties A et B sont indépendantes)
A, B, C, M ont pour affixes respectives a = 2, b = 1 – i 3 , c = -2 – 2i , z
M
*
(z*) est l’image de M(z) par la rotation de centre O, d’angle π
3
M’ (z’) est l’image de M
*
(z*) par la translation de vecteur 2
→
OU.
On note T la transformation qui transforme M en M’.
A. Ecriture complexe de T
1) Donner l’écriture complexe de la rotation, de la translation, et de T.
2) Prouver que T admet un seul point fixe.
3) En déduire une autre écriture complexe de T, sa nature et ses éléments caractéristiques.
B. Image d’un point
1) Déterminer l’affixe c’ de C’ = T(C).
2) Ecrire sous forme algébrique c’
c
3) En déduire la nature et l’aire de OCC’.
4) Quel(s) est(sont) l(es) antécédent(s) de B par T ?
C. Triangle rectangle
1) Avec z = x + iy, exprimer les parties réelles et imaginaires de z’, en fonction de x et y.
2) Déterminer et tracer l’ensemble des points M tels que OMM’ est rectangle en O.
EXERCICE 3 :
A et B ont pour affixes respectives 1 et 4. f est l’application qui a tout point M ( M ≠ A) d’affixe z associe le point M’
d’affixe z’ telle que z’ = f(z) = z – 4
z – 1
1) C a pour affixe i 2. Déterminer l’affixe de C’ = f(C)
2) Prouver que f admet deux points invariants (c.a.d f(M) = M), notés I et J avec Im(I) >0
3) Placer les points A, B, C, C’, I, J dans le plan complexe.
4) Quel est l’ensemble E des points M(z) qui sont tels que |z’| = 1 ? Le représenter.
5) Quel est l’ensemble F des points M(z) qui sont tels que z’ est réel ? Le représenter.
6) Quel est l’ensemble G des points M(z) qui sont tels que z’ est imaginaire pur ? Le représenter.
EXERCICE 4 :
1) Résoudre dans C les équations
(E
1
) z
3
– 1 = 0 (E
2
) z² – 2zcos(θ) + 1 = 0
2) On note j une des solutions complexes de (E
1
). Etablir les résultats suivants :
a.
→
j = j²
b. 1 + j + j² = 0
c. Déterminer les angles du triangle formé par les points d’affixes 1, j, j²
EXERCICE 5 :
1) Prouver que pour tous complexes z et z’, |z + z’|² + |z – z’|² = 2|z|² + 2|z’|²
2) Interpréter géométriquement ce résultat.

Correction
Exercice 1 :
1) z
1
= 4exp(2iπ
3) z
2
= 3 2 exp(iπ
4) z
3
= 2 2
3exp(5iπ 12) z
4
= 4
8
3
3
2
3
exp(- iπ
12)
2) z
3
= 3 – 1
3 + i 3 + 1 3
3) cos(5π
12) = 3 – 1 3 3 2 4 = 6 – 2 4 sin(5π 12) = 3 + 1 3 3 2 4 = 6 + 2 4
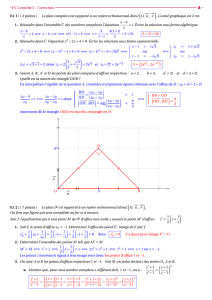
4) Construction
Construire 2 avec un triangle rectangle de côtés 1 et 1 puis 6 à l’aide de triangles rectangles de côtés 2 et 1 (=> 5
) puis 5 et 1 (=> 6) puis user et abuser du compas.
Pour diviser par 4 on construit 2 médiatrices successives.
Exercice 2 :
A.
1) Rotation : z* = exp(iπ
3) z
Translation : z’ = z* + 2
T : = z’ = exp(iπ
3) z + 2
2) On résout z’ = z et on obtient ω = 2exp(iπ
3)
3) z’ = exp(iπ
3) (z – 2exp(iπ 3)) + 2exp(iπ 3) Rotation de centre d’affixe ω et d’angle π 3.
B.
1) c’ = (1 + 3)(1 – i)
2) c’
c = 3 + 1 2 i
3) Arg (c’
c) = π 2 = (
→
OC ;
→
OC’) donc OCC’ rectangle en O |c’
c| ≠ 1 donc OCC’ non isocèle.
4) On résout 1 – i 3 = exp(iπ
3) z + 2 soit z = -2. L’antécédent de B est le point d’affixe -2
C.
1) T(x + iy) = (1
2x – y 3 2 + 2) + i(x 3 2 + y 2)
2) On résout donc OM² + OM’² = MM’² soit |z|² + |z’|² = |z – z’|²
 x² + 4x + y² = 0 (x + 2)² + y² = 4  M ∈ C(-2 ; 2)
EXERCICE 3 :
1) c’ = 2 + i 2
2) z = z – 4
z – 1  z
J
= 1 – i 3 ou z
I
= 1 + i 3
3) E = médiatrice de [AB] privée de A
4) F = (AB) privée de A car (
→
AM,
→
BM) = 0 [π]
5) G = cercle de diamètre [AB] privé de A car (
→
AM,
→
BM) = π
2 [π]  ABM rectangle en M
EXERCICE 4 :
1) 1 est racine évidente z
3
– 1= (z – 1)(z² + z + 1) = 0 z = 1 ou z = j ou z = j
(il manque un « z ») z = e
iθ
ou z = e
-iθ
2) Classique, les angles sont π
3
EXERCICE 5 : Utiliser |z|² = z z