Chapitre 11

Chapitre 11
FONCTIONS AFFINES
1°/ Forme algébrique
Le processus, qui à un nombre x, fait correspondre le nombre ax + b (où a et b sont des nombres
fixés) est appelé fonction affine.
 On la note f : x
ax + b
ou
f(x) = ax + b.
 Le nombre f(x) est l’image de x par la fonction f.
 f(x) = ax + b est appelée forme algébrique de la fonction affine.
Exemples : soit la fonction f définie par f(x) = - 3x +5. Quel est l’image des nombres 6 ; - 4 et
4/5 ? Quels sont les nombres qui ont pour images 14 et -22 par la fonction f ?
f(6) =-3  6 + 5
f(-4) = -3  (-4) + 5
f(Error!) = -Error!+ 5
f(6) = -13
f(-4) = 17
f(Error!) = Error!
Soit x tel que : f(x) =14
Soit x tel que : f(x) = -22
-3x + 5 =14
-3x + 5 = -22
-3x = 9
-3x = -27
d’où x = -3
d’où x = 9
2°/ Représentation graphique
Les fonctions affines sont représentées par des droites. Les fonctions linéaires sont des
fonctions affines (cas où b = 0).
Dans la forme algébrique f(x) = ax + b,
 b est appelé ordonnée à l’origine (intersection de la droite avec l’axe des ordonnées).
 a est appelé coefficient directeur de la droite (pente de la droite).
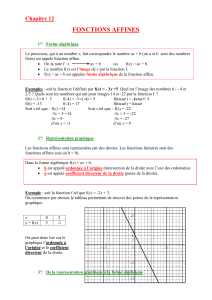
Exemple : soit la fonction f tel que f(x) = -2x + 3.
On commence par dresser le tableau permettant de trouver des points de la représentation
graphique.
x
y = f(x)
0
3
10
2
-1
On peut donc lire sur le
graphique l’ordonnée à
l’origine et le coefficient
directeur de la droite.
5
b
J
-10
O
I
-5
3°/ De la représentation graphique à la forme algébrique
-10
10
Pour trouver la forme algébrique d’une fonction affine à partir de sa représentation graphique,
on doit disposer des coordonnées de deux points. On doit alors calculer les valeurs de a et b.
On détermine a par la formule suivante : a = Error!
avec x1 ≠ x2.
Exemples :
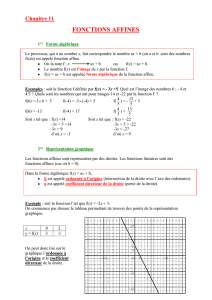
 Soit la fonction affine f représentée par la droite ci-dessous. Déterminer les
coordonnées de deux points de cette représentation, puis trouver sa forme algébrique.
A(- 4 ; +4) et B(+5 ; - 2)
Calculons le coefficient directeur a :
a = Error!
10
a = Error!
d’où a = - Error!.
Calcul de b : 4 = - Error!  (- 4) + b
b = 4 – Error!
b = Error!
d’où b = Error!
A
5
J
La forme algébrique de la fonction
est donc : f(x) = - Error!x +
-10
O
I
10
B
Error!
-5

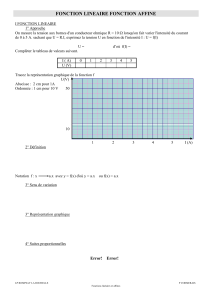
Déterminer graphiquement la forme algébrique de la fonction dont voici la représentation
graphique.
-10
A
2
J
O
-2
I
2
B
-4
Cette fonction est une fonction affine. Quand on se décale d’un cran vers la droite, on se
décale de 4 crans vers le bas. De même, la droite passe par le point de coordonnées (0 ;2).
Donc on a f(x) = - 4x + 2