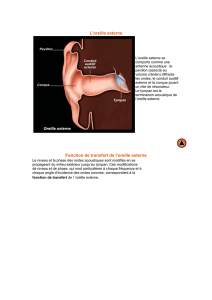
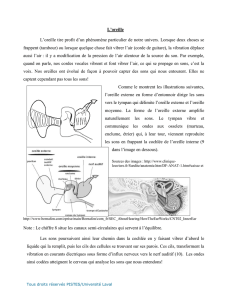
Le Décibel Insaisissable

L’oreille est sensible à des pressions allant de 0.00002 Pa à 20 Pa, soit un rapport de 1 à 1 000
000. Pour ramener cette large échelle de pression à une échelle plus réduite qui exprime mieux la
sensibilité de nos oreilles aux variations de niveau sonore, on a adopté la notation logarithmique et
créé le décibel ( DB ). (voir aussi les limites de la perception)
LOI DE WEBER - FECHNER
Lp est exprimé en DB , P est exprimé en Pa,
P0 est la pression de référence = 20 millionième de Pa
Une pression de 1 Pa représente 94 DB
Du fait de l’échelle LOGARITHMIQUE, on ne peut pas ajouter ARITHMÉTIQUEMENT les décibels de deux bruits pour
arriver au niveau sonore global. Quand l’écart entre les deux bruits est supérieur à 10dB, le niveau total des deux bruits est
quasiment celle du plus fort exprimé en DB. Si les deux bruits on la même puissance le niveau augmente de 3 DB.
Une augmentation de 10 DB du niveau sonore est perçue par nos oreilles comme un doublement du niveau sonore! Ceci
explique pourquoi la différence de puissance subjective entre un ampli de 100 W et de 200 W est apparemment plutôt
faible, et qu'il vaut en mieux investir dans la qualité des Watts que dans la quantité.
Le tableau si dessous donne pour chaque niveau de bruit la puissance électrique appliquée à une enceinte acoustique
ayant un rendement de 90 DB pour 1 w à une distance de 1 M (90 DB/W/M). Chaque fois que le rendement de l'enceinte
diminue de 3 DB il faudra doubler la puissance de l'ampli pour atteindre le même niveau sonore (pour un rendement de 84
DB/1W/1M il faut 40 W pour atteindre les 100 DB, un amplis de 200 W est nécessaire pour avoir une réserve de
puissance), inversement si les HP ont 3 DB de plus la puissance nécessaire est divisée par deux (pour un rendement de 93
DB/1W/1M il faut juste 5 W pour atteindre les 100 DB, un ampli de 25 W ou plus aura une réserve suffisante)
NATURE DES BRUITS
DESCRIPTION
DB
W
TURBO - RÉACTEUR
Troubles définitif
130
10 KW
MARTEAU - PILON
Seuil de la douleur
120
1000 W
RIVETEUSE
insupportables
110
100 W
MARTEAU PIQUEUR à 3 m
très pénibles
100
10 W
MOTO SANS SILENCIEUX
pénibles
90
1 W
RUE A GRANDE CIRCULATION
désagréable
80
0.1 W
RÉFECTOIRE BRUYANT
supportable
70
10 mW
GRANDS MAGASINS
bruyant
60
1 mW
RUE TRANQUILLE
Bruits courants
50
0.1 mW
BUREAU TRANQUILLE
agréable
40
0.01 mW
JARDINS CALMES
Calme
30
10 yW
STUDIO D’ENREGISTREMENT
Très calme
20
1yW
CHAMBRE SOURDE
Silence inhabituel
10
0.1 yW
SEUIL D’AUDIBILITÉ
Niveau théorique
0
0.01 yW
Pour les appareils de reproduction sonore
Un ampli capable de fournir 1000 W / 8 Ohms doit aussi reproduire correctement un signal 10
milliardième de Watt. L'enceinte avec un rendement de 90 DB/1W/1m.devrai supporter ces 1000

W pendant au moins 10 millisecondes Voila ce que j'appelle de la technologie de pointe,
heureusement que la pratique démontre qu'une puissance maximale un peut plus réduite (110
DBA soit 100W) est plus que suffisante. La limite inférieure est aussi difficile à atteindre, mais
heureusement le bruit de fond résiduel d'une pièce très calme dépasse souvent les 30 DB
acoustique, et de toute façon notre organisme produit un bruit d'une bonne dizaine de DB
(respiration, battement cardiaque, bruit circulatoires etc..)
Si vous faites un petit calcul vous comprendrez maintenant que le CD avec ses 16 Bit donne une
dynamique de 96 DB et une limite haute à 20 kHz) est un peu juste, pour tout appareil numérique il
faut 20 Bit et au moins 48 kHz (dynamique de 120 DB et une limite haute à 22.5 kHz) pour
dépasser réellement les limites de la perception humaine (si aucun autre défaut ne vient perturber
ces performances !)
Pour les appareils analogiques une électronique de préamplification de très bonne qualité y
parviennent tout juste, l'amplificateur de puissance a quelques difficultés au niveau des 120 DB de
dynamique, si l'enceinte à beaucoup plus de 90 DB de rendement, le bruit de fond risque d'être
trop élevé. Si l'enceinte a moins que 85 DB de rendement il faut que sa puissance dépasse 500 W
! (il faudrait aussi écrire une page dédiée au problème du couplage Ampli/Enceinte )
Les limites de la perception
Limite basse: Dans le grave elle a longtemps été fixée à 16 Hz. Les études les plus récentes
démontrent qu’a un niveau acoustique de 110 DB les fréquences inférieures a 30 Hz ne sont plus
perceptibles par la plupart des auditeurs. Il est donc inutile de vouloir reproduire des sons plus
graves, il est déjà assez difficile d’atteindre ces fameux 30 Hz avec une bonne qualité de
reproduction et une tenue en puissance suffisante.
Par contre les vibrations de moins de 20 à 60 Hz sont perçues par le corps humain
(particulièrement les parois de l'abdomen) le sens du touché détecte de vibration comprises entre
100 et 600 Hz (les pieds en contact avec le sol, ou les mains, ou votre postérieur sur son siège !)
.Il existe un moyen pour augmenter les sensations dans l'extrême grave, ce sont des vibreurs à
visser sous les sièges (Bass-Pump par exemple) qui transmettent les vibrations à votre corps et
donnent une impression de surpuissances des sons graves (ce n'est pas de la HI-FI, à
déconseiller pour la musique classique bien entendu !).
Les sons musicaux sont en général un mélange complexe de sons de déférentes fréquences, il à
été démontré que nous "entendons" la fondamentale (la plus basse d'entre elle et souvent la plus
puissante) même si elle n'est pas reproduite. L'explication est que notre cerveau corrige ce que
nous percevons réellement au point de reconstituer la partie manquante quand c'est possible, une
raison de plus de préférer un bon HP capable de descendre proprement à 30 ou 40 Hz à un
monstre hors de prix reproduisant les 16 Hz avec probablement de qualité moyenne pour les
fréquences plus élevées.
Pour les aigus, si ne niveau est assez fort, la limite se situe entre 18 000 Hz et 20 000 Hz dans
les meilleurs cas. En vieillissant cette limite à tendance à diminuer et se rapproche de 16 000 Hz.
La perception des sons aigu diminue très vite en cas de détérioration même partielle et légère de
l'oreille (voir L'oreille)
Le découpage des fréquences: La sensation de variation de hauteur est la même chaque fois
que la fréquence double, c'est pourquoi les musiciens utilisent la notion d'octave correspondant à
l'intervalle entre deux sons dont le plus aigu a la fréquence double du son plus grave. L'octave le
plus grave va de 16 Hz à 32 Hz, seul les grandes orgues et les instruments électroniques sont
capables de produire des sons aussi graves. L'octave suivant est plus encombré avec le basson,
le tuba basse, la grosse caisse, le piano, la contrebasse et la harpe. A l'autre extrémité le picolo, le
piano et le violon joue des notes un peu au dessus de 4000 Hz, seul certains orgues dépassent 8
000 Hz, par contre les harmoniques de nombreux instruments s'étalent un peu au delà de 16 000
Hz ! Entre ces deux limites une oreille très exercée (un musicien) est capable de distinguer 1400
hauteurs musicale différentes .(différence de fréquence inférieure à 1%)

Puissance :Pour compliquer le tout nos oreilles n'ont pas la même sensibilité pour toutes les
fréquences, les courbes de Flechter indique pour toutes les fréquences le niveau réel qui donne la
même impression de puissance qu'à 1000 Hz. Vous constater que pour les niveau faibles les
courbes se déforment de plus en plus et traduisent le fait que la sensibilité aux graves et aux aigus
diminue plus vite que pour les fréquences moyennes.(voir Les décibels) Dans l'extrême grave
nous avons plus de mal à distinguer les petites variations de puissance, certains concepteur de HI-
FI utilisent cette particularité pour concevoir des circuit électroniques qui limitent le niveau des
fréquences inférieures à 100 Hz en juste dessous du maximum supporté par les HP. Par contre
dans le médium il est possible à une oreille exercée de distinguer par comparaison directe plus de
250 niveaux d'intensité différents (c'est une résolution supérieure à 0.5 DB)
Le décibel
Voilà une unité de mesure que vous allez employer quotidiennement. Utilisé à tout va il sert souvent d'argument définitif
lors des discussions ou sur les affiches publicitaires. Il est important de bien le maîtriser.
Comme son nom l'indique, le décibel est le dixième du Bel. On a donné ce nom à cette unité en hommage à Alexander
Graham Bell. Nous voilà sacrément avancés non ? Avant d'aller plus loin sur cette merveilleuse unité qui est très simple
d'emploi malgré les apparences, effectuons un petit retour en arrière et regardons in instant les logarithmes.
Vous possédez sans le savoir, (peut-être) un merveilleux instrument de mesure logarithmique sur vous, je pense à votre
oreille. Celle-ci ne vous restitue pas linéairement les variations de puissance auditive de votre environnement.
Si, quand vous écoutez de la musique sur votre chaîne haute fidélité, vous multipliez par 10 la puissance émise par votre
amplificateur, votre sensation physiologique vous indiquera seulement un doublement de la puissance sonore.

Vous voyez ci-dessus l'allure d'une courbe logarithmique. En clair
cela signifie que les "x" évoluent beaucoup quand parallèlement
les "y" évoluent peu.
Ceci pourrait être la courbe de réponse de votre oreille à
une excitation sonore. sur l'axe des "x" vous trouvez
l'augmentation de puissance, sur les "y" la sensation
physiologique
Notation :
Vous êtes habitué à compter en base 10 (0,1,2,3,4,5,6,7,8,9) depuis votre plus tendre enfance, ceci ne vous empêche pas
de savoir qu'il existe d'autres bases comme la base 2 que nous avons étudié.
Il en va de même pour les logarithmes et l'on distinguera :
Le logarithme naturel de base "e".
Il est noté log.
C'est le seul, le vrai, la référence. Si vous trouvez des résultats
abracadabrants, il est à parier que votre tableur ou calculatrice
ne connaît que ceux-ci alors que vous désiriez le log en base 10.
Soyez attentifs à ces petites facéties.
e= 2,72
( valeur approchée)
On utilise en radioélectricité le logarithme de base 10. On passe du logarithme naturel au logarithme en base 10 par un
opération simple qui consiste à diviser comme suit :
log X
Log (10) X = ________
log 10
ce qui pourra s'énoncer comme suit:
le Logarithme en base 10 du nombre X sera égal au
logarithme base e de X divisé par le logarithme base e de
10
Vous remarquerez que l'on note les logarithme base e avec un petit "l"(log) et les Log base 10 avec un grand
"L". On trouve souvent aussi comme notation pour les base e "ln"
Exemple :
Calculons le Log base 10 de 1000 :
nous posons :
log 1000 6,9077
Log (10) 1000 = ________ = __________ = 3
log 10 2,30025
Pourquoi utiliser des décibel ?
Revenons sur l'acoustique est essayons de mesurer le rapport entre le plus fort signal auditif supportable par un être
humain et le plus faible. Le bruit est dû à une onde de pression. La pression la plus faible entendue par une oreille humaine
se situe vers 20.10-6 Pa.
Le signal le plus fort et encore supportable avoisine les 200 000 000 10-6 Pa.
Si nous calculons le ratio du signal le plus fort sur le plus faible, nous obtenons un rapport de 10 000 000, avouez que ce
n'est guère commode à manipuler. SI nous calculons le Log de ce rapport nous trouvons R = 7 ce qui revient à dire que ce
rapport est égal à 7 Bel
D'où vient le décibel ?
Nous venons de voir avec l'exemple précèdent que 7 Bel représentent un rapport de 100 000 000. Le bel est une "grosse"
unité, il est bien plus commode de mesurer avec une unité plus fine comme le décibel qui est le 10ème du Bel. Dans notre
exemple notre rapport serait de 70 dB, c'est mieux non ?
Les décibels et la radio :
Nous avons souvent, en radioélectricité des écarts comme celui cité en exemple concernant l'oreille humaine. Prenez le
plus petit signal perceptible par un récepteur et le plus fort , l'écart est encore plus important. Nous avons également
besoin de quantifier les gains et les atténuations et il est plus commode de parler d'un amplificateur de 20 dB de gain que
d'un amplificateur qui amplifie 100 fois. Nous avons également besoin de pouvoir ajouter ou soustraire des gains et des
atténuations, avec le dB c'est ultra simple car les logarithmes ont cette merveilleuse propriété de pouvoir transformer les
multiplications en additions et les divisions en soustractions. Nous avons besoin de pouvoir donner un niveau de puissance
par rapport à une référence fixe, le décibel par rapport au Watt ou mW le permet. Vous l'aurez compris cette unité
endémique de la radio est indispensable.
Définitions :

En puissance
Le dB est 10 fois le logarithme base 10 du rapport de puissance
P1/ P2.
P1
dB = 10 Log ______
P2
En tension ou courant
Le dB est 20 fois le logarithme base 10 du rapport des tensions
V1/V2 ou des courants I1/I2
V1
dB = 20 Log ______
V2
Exemple 1 :
quel est l'amplification de puissance exprimée en dB d'un
amplificateur qui sort 20 W pour 1 W à l'entrée ?
20
A = 10 Log ______ = 13 dB
1
Exemple 2 :
quel est l'atténuation de puissance exprimée en dB d'un
atténuateur auquel on applique un e puissance de 100 W et qui
restitue 15W
15
A = 10 Log ______ = - 8,2 dB
100
Exemple 3 :
quel est l'amplification de tension exprimée en dB d'un transistor
monté en amplificateur sur lequel on mesure 3 V de tension de
sortie pour 10 mV de tension d'entrée ?
3
A = 20 Log ______ = 49,5 dB
0.01
Note : Assurez-vous quand vous faites ces calculs d'utiliser les mêmes unités. On ne peut pas calculer avec des unités
hétéroclites.
Pour votre culture personnelle, quelques propriétés des logarithmes :
 Log ( A x B) = Log (A) + Log (B)
 Log ( A/B) = Log (A) - Log (B)
 si Ab = C alors log(a) C = B ( 102 = 100 équivaut à Log (10) 100 = 2 )
 log Ab = B x log A
Application pratique des log en radioélectricité :
Vous avez ci dessus une chaîne d'amplificateurs et d'atténuateurs. Connaissant l'atténuation ou le gain de chaque élément,
il est très facile de calculer le gain/atténuation total.
 1er cas en dB:
+10 - 3 +6 + 3 -20 = -4dB
globalement cette chaîne atténue le signal appliqué en entrée
 2ème cas avec les rapports de puissance
10 x 0,5 x 4 x 2 x 0,01 = 0,4
Vérifions simplement en calculant 10 Log 0,4 = -4 dB
C'est extrêmement commode car beaucoup de données vous sont fournies en dB. Prenez l'atténuation d'un câble coaxial,
on vous fournit l'atténuation en dB pour 100 m, il est aisé connaissant votre longueur d'en déduire la perte apportée.
Et l'opération inverse pour déterminer le rapport connaissant la valeur en dB ?
Connaissant la valeur en dB nous souhaitons déterminer la valeur
du rapport.
Il existe au moins deux méthodes pour parvenir au
résultat. Sans démonstration voici les résultats.