Document

P a g e | 1
Mouvement d’un palet Document : M.Moppert - CPF - Beyrouth
O
A
B
x
i
propulseur
k
z
G2
G3
G5
O
G0
G1
A
G4
x
TS
Physique
Mouvement d’un palet
Exercice résolu
Enoncé
- Les trois parties sont indépendantes.
- Valeur du champ de pesanteur : g = 9,80 m.s-2
Un palet en acier de masse m = 50,0 g peut se
déplacer sans frottement sur un plan incliné d’un
angle = 28,0° avec l’horizontale. Parti du point
O, le centre d’inertie G du palet passe au point A
avec une vitesse
A
v
acquise grâce à un propulseur
à ressort situé en bas du plan incliné (entre O et
A, le propulseur exerce une force
F
sur le
palet). En ce point, la palet est libéré avec une
vitesse de valeur vA= 2,00 m .s-1 et glisse
jusqu’au point B où il arrive avec une vitesse
nulle. Le palet poursuit alors son mouvement en
réalisant une chute verticale libre dans l’air.
A. Première partie : propulsion du palet entre O et A
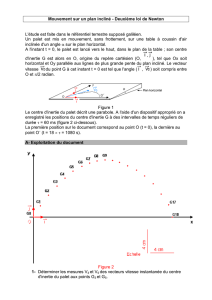
On filme le mouvement du palet entre O et A, puis on exploite la vidéo avec un logiciel adapté. La
figure ci-dessous, à l’échelle ½, représente la position qu’occupe le centre d’inertie G du palet à
intervalles de temps réguliers = 20,0 ms (points G0 à G5).
1. En exploitant la figure ci-dessus, déterminer les valeurs v2 et v4 des vecteurs vitesse aux
points G2 et G4.
2. Exprimer le vecteur accélération
3
a
du palet au point G3 en fonction de
2
v
,
4
v
et de
l’intervalle de temps , puis calculer sa valeur a3.
3. Faire le bilan des forces extérieures qui s’appliquent sur le système {palet} et les représenter
au point G sur le schéma en annexe.
4. a) Appliquer la deuxième loi de Newton et donner l’expression du vecteur accélération
G
a
du
centre d’inertie du palet.
b) Dans le repère (O,
i
), le vecteur accélération a pour expression :
G
a
=ax.
i
. Donner
l’expression de ax en fonction de m, g, F (valeur de la force
F
) et 
c) Pourquoi peut-on affirmer que ax =
G
a
(valeur du vecteur accélération) ?
d) En utilisant la valeur a3 de l’accélération trouvée à la question 2, calculer F au point G3.

P a g e | 2
Mouvement d’un palet Document : M.Moppert - CPF - Beyrouth
G
x
B. Deuxième partie : montée du palet entre A et B
1. Faire le bilan des forces extérieures qui s’appliquent sur le système {palet}.
2. Après avoir appliqué puis projeté la deuxième loi de Newton dans le repère (O,
i
), donner
l’expression de ax en fonction de g et . En déduire la nature du mouvement de G.
3. Dans le repère (O,
i
), le vecteur vitesse du centre d’inertie du palet a pour expression :
G
v
= vx.
i
.
a) En prenant comme origine des temps la date à laquelle le point G est en A, donner l’expression
de vx en fonction de t.
b) Calculer la durée nécessaire au point G pour aller de A à B.
C. Troisième partie : chute du palet
On prend maintenant comme origine des temps la date à laquelle G est en B et on travaille dans le
repère (B,
k
).
1. a) En appliquant la 2ème loi de Newton, donner l’expression du vecteur accélération
G
a
du
centre d ‘inertie du palet et de sa coordonnée az dans le repère (B,
k
).
b) En déduire la nature du mouvement de G.
2. a) Dans le repère (B,
k
), établir l’expression de la coordonnée vz du vecteur vitesse
G
v
puis de
la coordonnée z du vecteur position
BG
du centre d’inertie du palet.
b) Déterminer la date à laquelle la valeur vG de la vitesse du palet sera égale à 1,96 m.s-1.
3. Le professeur de physique d’une classe de TS dit à ses élèves : « Vous venez d’étudier la
chute du palet. Pourriez-vous décrire la chute de deux objets, l’un étant beaucoup plus lourd que
l’autre, dans un tube dans lequel on a préalablement fait le vide ? ». L’un des élèves répond :
« L’objet lourd tombera plus vite que l’objet léger ». Que penser de cette réponse ?
Annexe

P a g e | 3
Mouvement d’un palet Document : M.Moppert - CPF - Beyrouth
G
x
P
F
R
Corrigé
A. Première partie : propulsion du palet entre O et A
1. En exploitant la figure ci-dessus, déterminer les valeurs v2 et v4 des vecteurs vitesse aux points G2 et G4.
On assimile la vitesse instantanée en un point Gi à la vitesse moyenne entre les points Gi-1 et
Gi+1 proches de Gi :
v2 =
13
GG
2
soit : v2 =
2
3
2, 4 10 2
2 20, 0 10
= 1,2 m.s-1
v4 =
35
GG
2
soit : v4 =
2
3
3,2 10 2
2 20,0 10
= 1,6 m.s-1
2. Exprimer le vecteur accélération
3
a
du palet au point G3 en fonction de
2
v
,
4
v
et de l’intervalle de temps ,
puis calculer sa valeur a3.
On assimile le vecteur accélération au point Gi avec le vecteur accélération moyenne entre les
points Gi-1 et Gi+1 proches de Gi :
3
a
=
42
vv
2
=> a3 =
42
vv
2
soit : a3 =
3
(1,6 1,2)
2 20,0 10
= 10 m.s-2
3. Faire le bilan des forces extérieures qui s’appliquent sur le système {palet} et les représenter au point G sur le
schéma en annexe.
P
: poids du palet
R
: réaction du plan incliné
F
: force de propulsion
Rq : les frottements sont négligés (cf. énoncé).
4. a) Appliquer la deuxième loi de Newton et donner l’expression du vecteur accélération du centre d’inertie du
palet.
2ème loi de Newton :
P
+
R
+
F
= m.
G
a
=>
G
a
=
RF
gmm
b) Dans le repère (O,
i
), le vecteur accélération a pour expression :
G
a
= ax.
i
. Donner l’expression de ax en
fonction de m, g, F (valeur de la force
F
) et
Par projection dans le repère (O,
i
) : Px + Rx + Fx = m.ax
Px = - m.g.sin ; Rx = 0 ; Fx = F
=> -m.g.sin + F = m.ax => ax =
Fg.sin
m
c) Pourquoi peut-on affirmer que ax =
G
a
(valeur du vecteur accélération) ?
Le mouvement de G est accéléré : le vecteur vitesse et les vecteur accélération sont dans le
même sens et ax > 0 => ax = aG.
d) En utilisant la valeur a3 de l’accélération trouvée à la question 2, calculer F au point G3.
F = m.(ax + g.sin soit : F = 50,0 x 10-3 x [10 + (9,80 x sin 28,0)] = 7,3 x 10-1 N

P a g e | 4
Mouvement d’un palet Document : M.Moppert - CPF - Beyrouth
B. Deuxième partie : montée du palet entre A et B
1. Faire le bilan des forces extérieures qui s’appliquent sur le système {palet}.
P
: poids du palet et
R
: réaction du plan incliné.
2. Après avoir appliqué puis projeté la deuxième loi de Newton dans le repère (O,
i
), donner l’expression de ax en
fonction de g et . En déduire la nature du mouvement de G.
2ème loi de Newton :
P
+
R
= m.
G
a
=> Px = m.ax => - m.g.sin = m.ax => ax = - g.sin
ax < 0 et ax = Cte : le vecteur accélération de G est un vecteur constant . Le mouvement est
rectiligne uniformément retardé.
3. Dans le repère (O,
i
), le vecteur vitesse du centre d’inertie du palet a pour expression :
G
v
= vx.
i
a) En prenant comme origine des temps la date à laquelle le point G est en A, donner l’expression de vx en fonction
de t.
G
G
dv
adt
donc le vecteur vitesse est une primitive du vecteur accélération et vx est une
primitive de ax.
Donc : vx = - (g.sin.t + vA
b) Calculer la durée nécessaire au point G pour aller de A à B.
Au point B, la vitesse de G est nulle : vx = 0 = - (g.sint + vA => t =
A
v
g.sin 
Soit : t =
2,00
9,80 sin28,0
= 4,35 x 10-1 s
C. Troisième partie : chute du palet
On prend maintenant comme origine des temps la date à laquelle G est en B et on travaille dans le repère (B,
k
).
1. a) En appliquant la 2ème loi de Newton, donner l’expression du vecteur accélération
G
a
du centre d‘inertie du
palet et de sa coordonnée az dans le repère (B,
k
).
Bilan des forces extérieures :
P
(poids du palet).
Rq : il s’agit d’une chute libre (cf. énoncé) donc toutes les forces dues à l’air sont négligées.
2ème loi de Newton :
P
= m.
G
a
=> m.
g
=>
G
a
=
g
Projection dans le repère (B,
k
) : az = - g
b) En déduire la nature du mouvement de G.
Le vecteur accélération est constant et dans le même sens que le vecteur vitesse : le mouvement
est rectiligne uniformément accéléré.
2. a) Dans le repère (B,
k
), établir l’expression de la coordonnée vz du vecteur vitesse puis de la coordonnée z du
vecteur position du centre d’inertie du palet.
G
G
dv
adt
donc le vecteur vitesse est une primitive du vecteur accélération et vz est une
primitive de az.
Donc : vz = - g.t (vitesse initiale nulle : cf. énoncé).
G
dBG
vdt
donc le vecteur position est une primitive du vecteur vitesse et z est une primitive de
vz.
Donc : z = -
2
1.g.t
2
(z = 0 à t = 0).

P a g e | 5
Mouvement d’un palet Document : M.Moppert - CPF - Beyrouth
b) Déterminer la date à laquelle la valeur vG de la vitesse du palet sera égale à 1,96 m.s-1.En déduire la valeur de
z à cette date.
Si vG = 1,96 m.s-1 => vz = - 1,96 m.s-1. Or : t =
z
v
g
soit : t =
1,96
9,80
= 2,00 x 10-1 s
=> z = -
12
19,80 (2,00 10 )
2
= 1,96 x 10-1 m
3. Le professeur de physique d’une classe de TS dit à ses élèves : « Vous venez d’étudier la chute du palet.
Pourriez-vous décrire la chute de deux objets, l’un étant beaucoup plus lourd que l’autre, dans un tube dans lequel
on a préalablement fait le vide ? ». L’un des élèves répond : « L’objet lourd tombera plus vite que l’objet léger ».
Que penser de cette réponse ?
La chute d’un solide dans le vide est indépendante de sa masse. Les deux objets tomberont à la
même vitesse.