correction

Le but de cet exercice est de vérifier la
2ème loi de Newton:
ext G
F = m.a
A Luttringer

2.1. Bilan des forces appliquées au palet en équilibre
•Son poids
–Vertical
–Vers le bas
–Appliqué en G
P
•La réaction de la table : elle
est perpendiculaire au support
car il n’y a pas de frottements
R
G
A 
P
R
Le système (palet ) est soumis à :
le système est en équilibre, donc :
P + R = 0

2.2. Bilan des forces appliquées au palet en mouvement
•En plus des 2 forces précédentes,
le palet est soumis à la force de
rappel du ressort.
F
Elle est :.
–horizontale
–Dirigée de G vers A
–Norme :
Avec:
lo : longueur initiale du ressort
R : rayon du palet
0
F = k(AG-l -R)
O
l
l0R
G
G
A 
A 
R
R
P
P
F

2.3. Si le référentiel est galiléen, on peut appliquer la seconde loi de
Newton
2.4.
Mais,
Donc :
G
P + R +F = m.a
P + R = 0
G
F = m.a

1
13
2G G 0,042
v 0,52m.s
2 2 0,040
1
35
4
G G 0,028
v 0,35m.s
2 2 0,040
2
v
4
v
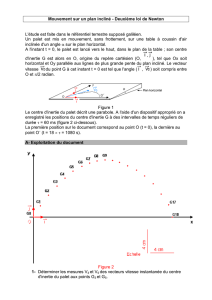
3.1.a Vecteurs vitesse en G2et G4