Modèle mathématique.

Relation trigonomètrique
dans le triangle quelconque
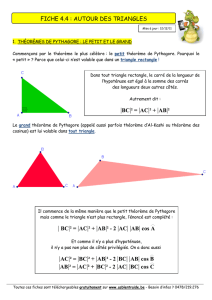
1) Théorème des sinus. a) Découverte du théorème.
Construire un triangle ABC tel que AB = 4,5 cm et AC = 5,5 cm.
Tracer la hauteur [AH].
Utiliser les relations trigonométriques, dans le triangle ABH, rectangle en H, pour exprimer sin
B
ˆ
:
sin  B = AH
AB
En déduire une expression de AH en fonction de sin
B
ˆ
et AB
Error!
Utiliser les relations trigonométriques, dans le triangle ACH, rectangle en H, pour exprimer sin
C
ˆ
sin  C = AH
AC
En déduire une expression de AH en fonction de sin
C
ˆ
et AC
Error!
En déduire la relation suivante :
C
AB
ˆ
sin
=
B
AC
ˆ
sin
D’après formules précédentes : AB sin  B = AC sin  C soit AB
sin  C  AC sin  C
Mesurer sur la figure, les angles
A
ˆ
,
B
ˆ
et
C
ˆ
et compléter le tableau suivant :
4,5
5,5
5,9
72 °
A
B
C

A
ˆ
=72 °
B
ˆ
= 62 °
C
ˆ
= 46 °
C
AB
ˆ
sin
A
BC
ˆ
sin
B
AC
ˆ
sin
Valeur exacte
Valeur arrondie à 10-1
près
6,2
6,2
6,2
Conclure.
Les résultats sont quasiment identiques, on peut donc conclure que les longueurs de
côtés sont proportionnelles aux sinus des angles opposés.
Tracer le cercle circonscrit au triangle.
Mesurer son diamètre. En déduire son rayon. On mesure = 6,2 cm soit R =
Error!
3,1
En déduire une égalité entre la relation suivante
C
AB
ˆ
sin
=
A
BC
ˆ
sin
=
B
AC
ˆ
sin
et le rayon R.
AB
sin  C  AC sin  B  BC sin  A = 2R
b) Définition.
Dans tout triangle, les longueurs des côtés sont
proportionnelles aux sinus des angles opposés.
a
sin A  b sin  B  c sin C
c) Dans quelle situation utiliser le théorème des sinus.
 Calculer la longueur d’un côté lorsque l’on connaît la mesure de deux angles et la longueur d’un côté.
 Calculer la mesure d’un angle lorsque l’on connaît la longueur de deux côtés et la mesure d’un angle
non compris entre ces deux côtés.
d) Applications.
 Calculer les longueurs du côté [AB] d’un triangle ABC tel que :
4,5
sin 46°
5,9
sin 72°
5,5
sin 62°

Résolution
a)
BC = 10 ;
A
ˆ
= 70° ;
C
ˆ
= 50°
FIGURE
b)
BC =8 ;
B
ˆ
= 50°;
C
ˆ
= 100°
FIGURE
 Calculer la mesure de l’angle
A
ˆ
d’un triangle ABC tel que :
a)
AB = 8 ; BC = 10 ;
C
ˆ
= 40°
FIGURE
b)
AB = 15 ; BC = 20 ;
C
ˆ
= 40°
FIGURE
2) Théorème des cosinus ou théorème de Carnot.
a) Découverte du théorème.

premier cas : Triangle quelconque dont tous les angles sont aigus.
Soit le triangle quelconque ABC.
Travail dans le triangle rectangle ABH.
Ecrire la relation de Pythagore pour le triangle rectangle ABH.
...............................................................…………………………………..
Exprimer BH en fonction de BC et HC.
……………………………………………………………………………..
Donner alors l’expression de AB².
...........................................................................................................………………………………
.…………………………………………………………………………………………. (1)
Travail dans le triangle rectangle ACH.
Ecrire la relation de Pythagore pour le triangle rectangle ACH.
…………………………………………………………………………..
Exprimer AH en fonction de AC et CH.
……………………………………………………………………………
Remplacer l’expression de AH² dans la relation (1).
……………………………………………………………………………
.....................................................................................…………………..
Exprimer CH en fonction de AC et de l’angle
C
ˆ
.
…………………………………………………………………………….
En déduire l’expression de AB² en fonction de AC, BC et
C
ˆ
.
……………………………………………………………………………….
deuxième cas : Triangle quelconque dont l’un des angles est obtus.

Exprimer BH en fonction de HC et BC.
……………………………………………………………………….
Exprimer AB² dans le triangle rectangle AHB.
.........................................................................................……………..
Exprimer AB² en fonction de AC, BC et HC.
....……………………………………………………………………..
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
Exprimer CH en fonction de AC et de l’angle
C
ˆ
.
………………………………………………………………………..
En déduire l’expression de AB² en fonction de AC, BC et
C
ˆ
.
………………………………………………………………………
Obtient-on le même résultat que dans le premier cas ?
………………………………………………………………………………………………………………..