algeabre lineaire_4

ALGEBRE LINEAIRE
III-ième SEMESTRE
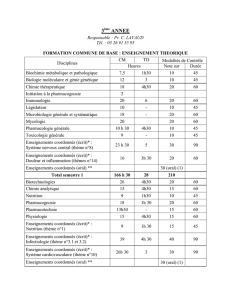
Volume horaire – contrôle des connaissances
Cours: 2 heures / semaine, 34 heures / semestre.
Travaux dirigés: 2 heures / semaine, 34 heures / semestre
Un colloque évalué à l’aide d’une note d’épreuve (écrite) et une note de travaux dirigés, qui est
déterminée sur la base de deux travaux de contrôle et un travail de calcul (un devoir à faire à
domicile):
Objectif du cours:
Les sujets traités sont indispensables aux futurs ingénieurs. L’objectif est de développer
l’aptitude des étudiants à concevoir et à mettre en oeuvre les notions et les méthodes de
l’Algèbre linaire et de la Géométrie analytique.
Méthodes:
L’enseignement alterne des cours théoriques et des travaux dirigés. Les travaux dirigés servent à
approfondir les problèmes traités pendant les cours et aident les étudiants à résoudre les
exercices.
Rapport avec les autres matières:
Les bases mathématiques acquises pendant l’enseignement secondaire sont indispensables. Les
mathématiques sont utilisées dans toutes les matières scientifiques.
Programme
Systèmes d'équations linéaires, méthode de Gauss, méthode de Jordan-Gauss.
Vecteurs, opérations linéaires, bases, coordonnés, systèmes de coordonnés, produits: scalaire,
vectoriel, mixte.
Lignes et surfaces: lignes données par leurs équations en coordonnés polaires, lignes données par
leurs équations paramétriques, droite dans l'espace, plan, surfaces de deuxième ordre, surfaces
cylindriques, surfaces de révolution, surfaces coniques.
Espaces linéaires, bases, dimension, coordonnés, changement de base.
Espaces euclidiens, orthogonalité, bases orthonormés, inégalités de Cauchy-Bouneacovsky et de
Mincovski.
Espaces affines,
systèmes de coordonnés, éléments de la Géométrie analytique ndimensionnelle.
Opérateurs linéaires, valeurs propres, vecteurs propres, diagonalisation.
Formes linéaires, formes bilinéaires, formes quadratiques, réduction à la forme canonique,
application à la géométrie analytiques.
Bibliographie
1.R.Cairoli, Algèbre linéaire, Presses polytechniques et universitaires romandes, Lausanne,
Suisse, 1991.
2.Iliin V.A., Pozneac E.J., Geometrie analitică, Cartea Moldovenească, Chişinău, 1990.
3.Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, Наука, Москва,
1985.
4.Ефимов А.В., Демидович Б.П., Сборник задач по математике для втузов. Линейная
алгебра и основы математического анализа, Наука, Москва, 1986.