LYCEE MARCEL RUDLOFF Principe Fondamental de la

LYCEE MARCEL RUDLOFF
Principe Fondamental de la Dynamique
Terminale GE
Mécanique
1/3
C’est l’étude des relations entre les mouvements d’un solide et leurs causes. Dans ce chapitre nous nous
limiterons à l’étude du mouvement de translation rectiligne d’un solide et du mouvement de rotation autour
d’un axe confondu avec l’axe d’inertie du solide.
I. Notion de repère galiléen :
 Repère absolu : C’est le repère fixe par rapport à l’ensemble de l’univers.
 Repère de Copernic : Son origine est le centre d’inertie du système solaire (proche du soleil) dont
les axes passent par des étoiles fixent entre elles. En mécanique classique, les vitesses sont
négligeables devant la vitesse de la lumière (300000 km/h), on admet donc que le repère de
Copernic est absolu).
 Repère galiléen : Repère animé d’un mouvement de translation rectiligne uniforme par rapport au
repère de Copernic.
Remarque : En négligeant la vitesse de rotation de la terre (1tour/24H) et en considérant le rayon de
courbure de la trajectoire elliptique de la terre très grand, on supposera le repère terrestre comme galiléen.
II. Principe Fondamental de la Dynamique :
Dans un repère galiléen % on considère un solide S modélisable par un point M de masse m soumis à des
actions mécaniques extérieures en M modélisées par le glisseur suivant :
M
MSSR
SS  0)/( :)/( 
Le Principe Fondamental de la Dynamique nous dit qu’à chaque instant t le solide S est soumis à une
accélération £M telle qu’en un point quelconque A :
A
m
m
SS
M
M
M
M
_AM
:)/(
a) Principe Fondamental de la Dynamique appliqué à un solide en translation :
Soit un solide S de masse m de centre d’inertie G en mouvement de translation soumis à des actions
mécaniques extérieures. L’expression du PFD au point G s’écrit :
G
G
G
G
G
m
/S)S(M
SS
SS  0
)/(
:)/( 
_
£R
En un point quelconque A :
ÄA([S/S) = ÄG([S/S) + _AG  m£G
A
m
m
SS
A
G
G
A
_AG
:)/(
= £0

LYCEE MARCEL RUDLOFF
Principe Fondamental de la Dynamique
Terminale GE
Mécanique
2/3
Remarques :
 Théorème de la résultante dynamique : £R([S/S) = m£G.
 Théorème du moment dynamique : ÄA([S/S) = _AG  m£G
 Pour un mouvement de translation rectiligne uniforme (MTRU) : £G = £0
G
G
SS  0
0
:)/( 
Cette relation est donc une condition nécessaire mais non suffisante pour définir l’équilibre d’un
solide (Principe Fondamental de la Statique)
 Pour un mouvement de translation rectiligne uniformément varié (MTRUV) : G = constante.
Exemple : Chute libre d’un solide
Soit S de masse m en chute libre. Soit £G le vecteur accélération du centre de masse G
Les actions mécaniques extérieures sont définies par le glisseur :
G
G
P
SS  0 :)/( 
PFD :
G
G
G
m
SS   0 :)/( 
Le théorème de la résultante dynamique nous donne : £P = m£G
Et avec £G = g (vecteur accélération de la pesanteur) nous avons : P = mg
Exercices : a) Une navette spatiale est supposée à l'arrêt dans l'espace. Les trois moteurs sont allumés. La poussée de chaque
moteur est de 2300kN, les trois poussées sont parallèles et leur action résultante passe par le centre de gravité G.
Déterminer l'accélération supportée par les astronautes si la masse de la navette est de 100 tonnes.
(réponse : a=69m/s²)
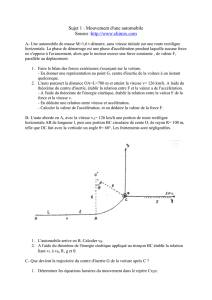
b) La figure ci-contre représente un dispositif de levage de containers de
semi-remorques.
Le container 6 de masse M6=20000kg est soulevé par l’intermédiaire de
quatre câbles 20 et 20’ en liaison pivot sans frottement.
Hypothèses :
- le repère (O, x, y, z) est galiléen.
- Le mouvement du container est rectiligne d’axe (A, y).
- Le mouvement de levage est accéléré tel que
s
msolG 2 /3.0)/6( 6
Appliquer le PFD et déterminer la tension dans un câble 20 ou 20’.
(réponse : I(20/6) = J(20’/6) = 54520 N)
III.
£P
G
É

LYCEE MARCEL RUDLOFF
Principe Fondamental de la Dynamique
Terminale GE
Mécanique
3/3
t (s)
rad/s (t)θ
150
0
0.75
III. Notion de moment d’inertie :
a) Moment d’inertie d’un solide par rapport à un axe :
Le moment d’inertie caractérise la répartition des masses d’un solide autour
d’un axe. Plus la valeur du moment d’inertie est grande, plus il sera difficile de
mettre le solide en rotation autour de cet axe.
Soit un solide S de masse m et un axe (O, z). Soient dm la masse d’un point Mi
 S. On appelle moment d’inertie de S par rapport à l’axe (O, z) le scalaire
positif suivant :
 )(
2
I(O, Sidmlz
Unité : le moment d’inertie s’exprime en kg.m²
b) Exemples :
 Cylindre plein :
 Sphère pleine :
IV. PFD appliqué à un solide homogène en rotation autour d’un axe de symétrie matériel fixe :
Dans le cas de la rotation d’un solide homogène S autour d’un axe de symétrie matérielle fixe (O, z)
appartenant à S, le PFD s’écrit en tout point O de cet axe :
O
O
O
OzOI
/S)S(M
SS
SS 
θz).
_
£R
,(
0
)/(
:)/(
avec
θ
= l’accélération angulaire du solide en rotation.
Remarques :
 Théorème de la résultante dynamique : £R([S/S) = 0
 Théorème du moment dynamique : ÄO([S/S) =
zOI  θz).,(
Exercice : On se propose d’étudier le couple de démarrage à vide d’un moteur électrique dont le rotor est modélisé par un cylindre
plein de masse m=3kg et de rayon 30 mm. On notera (O, z) l’axe de symétrie matérielle du rotor. Soit le graphe du mouvement de
S suivant :
 Nature du mouvement et valeur de l’accélération en phase de démarrage ?
MRUV avec ’’ = 200 rad/s²
 Calculer le moment d’inertie du rotor par rapport à (O, z)
I(O, z) = 1,35.10-3 kg.m²
 Calculer la valeur du moment par rapport à l’axe (O, z) des actions
mécaniques agissant sur S pendant le démarrage à vide. MOz([S/S) = 0.27
Nm
z
O
Mi
S
li
x
z
O
I(O, z) = ÂM.R²
Avec M la masse du cylindre et R son rayon
I(O, z) =
MR2
5
2
O
x
z
y