Le décibel

Le décibel
L'oreille humaine permet d'écouter des sons extrêmement faible comme le bruit d'une goutte d'eau
s'écrasant sur le sol d'une grotte silencieuse aussi facilement que le vacarme épouvantable des chutes
du Niagara.
L'étendue des puissances de sons audibles est gigantesque : combien de gouttes d'eau s'écrasent à
chaque instant dans une cataracte ? Des milliards ? Des milliards de milliards ? Inutile de faire le
calcul. Pourtant on ne peut pas dire que le son d'une cataracte soit des milliards de milliards plus fort
que celui de la simple goutte : c'est que l'impression de puissance d'un son n'est pas directement
proportionnel à la puissance.
Prenons un exemple : si l'on admet qu'un duo de 2 violons produit un bruit de "force" 1, il faudra un
orchestre de 4 violons pour que l'oreille perçoive un bruit deux fois plus grand, que nous noterons de
force 2. Avec 8 violons l'effet produit sera de force 3 et avec 16 il sera de 4, et ainsi de suite...
Dans un récepteur
Sur la bande 2M (144.0 MHz à 148.0 MHz), un signal reçu S9 (un niveau considéré comme déjà
très fort) représente une puissance d'environ 1pW (1 picowatt = 10-12 W) à l'entrée du récepteur. Pour
être audible confortablement, il faudra qu'il soit amplifié par le récepteur de façon à représenter une
puissance de 1W dans le haut-parleur. La puissance du signal a été amplifiée 1000000000000 fois.
Ce nombre astronomique n'a rien d'extraordinaire pour un récepteur VHF qui devra rendre audible
des signaux 100000 fois plus faibles encore.
La manipulation de tous ces zéros donne le vertige et peut être la source d'erreurs dans les calculs.
Heureusement que les logarithmes ont permis la naissance d'une unité de gain et d'affaiblissement plus
pratique à utiliser : le décibel.
Gain en puissance d'un amplificateur
Soit un amplificateur de gain A =
Error!
où Ps est la puissance de sortie et Pe est la puissance
d'entrée de l'amplificateur. Ces deux puissances doivent être exprimées dans la même unité.
Le gain en décibel d'un amplificateur est donné par la formule G = 10 Log A soit G = 10 Log
Error!
.
A étant un nombre sans unité exprimant le rapport de puissances
Error!
.
Le décibel est le dixième du bel, ainsi nommé en l'honneur de Graham Bell, l’inventeur du
téléphone.
Exemple : le récepteur évoqué ci-dessus a un gain en puissance de 1 000 000 000 000 ou 10 12.
Sachant que log(1012) = 12, le gain en décibel est G = 10 x12 soit G = 120 dB.
Le tableau ci-dessous donne quelques gains en dB pour différents rapport A=
Error!
.

A
G(dB)
A
G(dB)
0,10
– 10
10,00
10
1,26
1
15,85
12
1,58
2
19,95
13
2,00
3
31,62
15
2,51
4
39,81
16
3,16
5
63,10
18
3,98
6
100
20
5,01
7
158
22
6,31
8
251
24
7,94
9
1000
30
On voit que :
- doubler la puissance correspond à un gain de 3 dB ;
- quadrupler la puissance correspond à un gain de 6 dB ;
- décupler la puissance correspond à un gain de 10 dB ;
- centupler la puissance correspond à un gain de 20 dB.
- Un gain de 10dB (A = 10) correspond à la somme de 7dB (A = 5,01) et de 3dB (A = 2), et
correspond au produit 5,01 2.
Gain en tension
La mesure d'une tension à l'entrée ou à la sortie d'un ampli ou d'un atténuateur est beaucoup plus
facile que la mesure d'une puissance. C'est pourquoi on essaie toujours de calculer les gains à partir du
rapport de tension A =
Error!
.
Cette méthode est valide à condition que l'entrée et la sortie aient la même impédance (par exemple
50 ohms).
Le calcul du gain devient donc G = 20 Log
Error!
.
Comme pour le rapport de puissance, un gain en dB négatif est un affaiblissement.
Exemple : l'amplitude d'un signal à l'entrée d'un câble coaxial est de 10 V et de 2V à la sortie. Le
rapport de tension est de 0,2. Le gain en décibel G = 20 Log(0,2) = 20 – 0,7, soit G = – 14 dB
Correspondance entre les rapports et le gain en dB
Le tableau permet de déterminer rapidement un gain en connaissant le rapport de puissance ou de
tension ou encore de trouver le rapport correspondant à un gain en dB.
Exemple 1 : un amplificateur fournit 10 W quand on applique 2 W à son entrée. Le rapport
Error!
est égal à 5 donc le gain de l'ampli est de 7dB.

Exemple 2 : on mesure une tension maximum de 4 V, à quelle tension correspond le niveau – 3dB ?
+ 3 dB correspond à un rapport
Error!
de 1,41.
Donc – 3dB est équivalent à un rapport
Error!
de
Error!
soit 0,70.
La tension correspondante est 4 0,70 = 2,8 V.
G(dB)
Error!
Error!
G(dB)
Error!
Error!
G(dB)
Error!
Error!
1
1,12
1,26
21
11,2
125,9
41
112
12589
2
1,26
1,58
22
12,6
158,5
42
126
15849
3
1,41
2,00
23
14,1
199,5
43
141
19953
4
1,58
2,51
24
15,8
251,2
44
158
25119
5
1,78
3,16
25
17,8
316,2
45
178
31623
6
2,00
3,98
26
20,0
398,1
46
200
39811
7
2,24
5,01
27
22,4
501,2
47
224
50119
8
2,51
6,31
28
25,1
631,0
48
251
63096
9
2,82
7,94
29
28,2
794,3
49
282
79433
10
3,16
10,00
30
31,6
1000,0
50
316
100000
11
3,55
12,59
31
35,5
1258,9
51
355
125893
12
3,98
15,85
32
39,8
1584,9
52
398
158489
13
4,47
19,95
33
44,7
1995,3
53
447
199526
14
5,01
25,12
34
50,1
2511,9
54
501
251189
15
5,62
31,62
35
56,2
3162,3
55
562
316228
16
6,31
39,81
36
63,1
3981,1
56
631
398107
17
7,08
50,12
37
70,8
5011,9
57
708
501187
18
7,94
63,10
38
79,4
6309,6
58
794
630957
19
8,91
79,43
39
89,1
7943,3
59
891
794328
20
10,00
100,00
40
100,0
10000,0
60
1000
1000000
En basse fréquence
Certains contrôleurs universels à aiguille possèdent une échelle en dB. Cette dernière permet la
mesure de niveau de signal en BF sur une charge de 600 ohms. Le niveau de référence 0 dB
correspond à une puissance de 1 mW, ce qui correspond à une tension de 0,775V sur une impédance
de 600 ohms.
Exemple : un amplificateur sort 1 W sur 600 ohms, le niveau de sortie sera de + 30dB. L'amplitude
du signal sera alors de 24,5 volts.
Si à l'entrée de cet ampli l'amplitude du signal mesurée sur 600 ohms est de 0,5 volts, la puissance
correspondante est de 0,42mW et le niveau de -3,7dB.
Utilisation du tableur

Il est facile d'utiliser un tableur pour réaliser des petits outils de calcul de gain, amplification et
atténuation.
Le fichier à télécharger (.ZIP - 10ko) contient une feuille de calcul de format StarOffice. Voir :
utilisation du tableur.
Physique du son
Son ou bruit ?
Tout ce qui vibre émet un son. Un corps
vibrant communique sa vibration, dans le
milieu récepteur (air, liquide, solide) sous la
forme d’ondes de pression et de dépression
de proche en proche de la source à l’organe
de réception qui peut être, par exemple,
l’oreille d’une personne.
La vitesse de propagation du son dépend du
milieu dans lequel il est émis.

Le son est caractérisé par quatre grandeurs :
le volume ou l'intensité, la tonalité, le timbre
et la durée d'apparition.
Le bruit est un mélange complexe de sons.
D'après l'AFNOR (Association Française de
Normalisation) :
le son est “une sensation auditive
engendrée par une onde acoustique”.
le bruit résulte d'un mélange complexe de
sons d'intensités et de fréquences différentes.
Il “correspond à tout phénomène acoustique
produisant une sensation généralement
considérée comme désagréable ou gênante”.
La nocivité d'un bruit dépend de l'intensité
du son et de la durée d'exposition.
??? en savoir plus ...
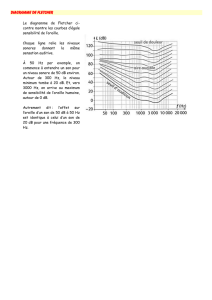
Les fréquences audibles
Nous n'entendons pas tous les sons.
L'oreille humaine est sensible aux sons
dont la fréquence est comprise entre 20
et 20000 Hz.
En dessous, ce sont des infrasons perçus
non plus comme des sons mais comme
des vibrations. Au delà, ce sont des
ultrasons, perçus uniquement par
certains animaux.La fréquence du son
est la caractéristique la plus importante
dans la comparaison des systèmes de
perception et d'émission sonores des
espèces.
Les espèces diffèrent par la gamme de fréquences qu'elles peuvent entendre et émettre.
La plupart des espèces perçoivent une gamme de fréquences plus large que celle qu'elles
peuvent produire.
Elles ne produisent que les sons qu'elles sont capables d' entendre.