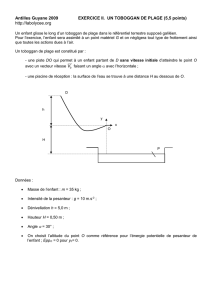
1 Systèmes oscillants

31
D EVOLUTION TEMPORELLE DES SYSTEMES MECANIQUES ............................................................................ 32
1 LA MECANIQUE DE NEWTON ........................................................................................................................................... 32
Le vecteur vitesse ............................................................................................................................................................................... 32
Deuxième loi de Newton (aspect semi quantitatif) ............................................................................................................................ 32
Accélération du centre d’inertie ......................................................................................................................................................... 32
Le repère de Frenet ............................................................................................................................................................................ 33
Première loi de Newton ..................................................................................................................................................................... 34
Rôle de la masse ................................................................................................................................................................................ 34
Deuxième loi de Newton appliquée au centre d'inertie ...................................................................................................................... 35
Référentiels galiléens ......................................................................................................................................................................... 35
Troisième loi de Newton : loi des actions réciproques ....................................................................................................................... 35
2 ETUDE DE CAS ................................................................................................................................................................ 35
2.1 Chute verticale d’un solide ....................................................................................................................................... 35
Champ de pesanteur ........................................................................................................................................................................... 35
Champ de pesanteur uniforme ........................................................................................................................................................... 36
Chute verticale avec frottement ......................................................................................................................................................... 36
Chute verticale libre ........................................................................................................................................................................... 38
Importance des conditions initiales .................................................................................................................................................... 38
2.2 Mouvement de projectiles dans un champ de pesanteur uniforme ............................................................................ 38
Equation de la trajectoire à partir des équations horaires paramétriques ............................................................................................ 39
Influence de la valeur de la vitesse initiale v0 sur la trajectoire du projectile ..................................................................................... 40
Influence de l’angle de tir  sur la trajectoire du projectile ............................................................................................................... 40
2.3 Satellites et planètes .................................................................................................................................................. 40
Lois de Kepler .................................................................................................................................................................................... 40
Référentiels héliocentrique et géocentrique ....................................................................................................................................... 41
Etude d’un mouvement circulaire uniforme ....................................................................................................................................... 41
Loi de gravitation universelle ............................................................................................................................................................ 41
Application de la deuxième loi de Newton au centre d’inertie d’un satellite ou d’une planète .......................................................... 41
Satellite géostationnaire ..................................................................................................................................................................... 42
L’impesanteur .................................................................................................................................................................................... 43
3 SYSTEMES OSCILLANTS .................................................................................................................................................. 43
3.1 Présentation de divers systèmes oscillants mécaniques ............................................................................................ 43
Le pendule simple .............................................................................................................................................................................. 43
Etude du mouvement du pendule simple ........................................................................................................................................... 43
3.2 Le dispositif solide ressort ......................................................................................................................................... 44
Force de rappel exercée par un ressort ............................................................................................................................................... 45
Etude dynamique du système ............................................................................................................................................................. 45
3.3 Le phénomène de résonance ..................................................................................................................................... 45
Influence de l’amortissement de l’oscillateur forcé ........................................................................................................................... 46
Notion de résonance de l’oscillateur forcé ......................................................................................................................................... 46
4 ASPECTS ENERGETIQUES ................................................................................................................................................. 47
Travail élémentaire d’une force ......................................................................................................................................................... 47
Travail d’une force extérieure appliquée à l’extrémité d’un ressort, l’autre extrémité étant fixe ....................................................... 47
Energie potentielle élastique du ressort .............................................................................................................................................. 48
Energie mécanique du système solide ressort .................................................................................................................................... 48
Energie mécanique d’un projectile dans un champ de pesanteur uniforme ........................................................................................ 48
5 L’ATOME ET LA MECANIQUE DE NEWTON : OUVERTURE AU MONDE QUANTIQUE ........................................................... 48
5.1 Limites de la mécanique de Newton .......................................................................................................................... 48
5.2 Quantification des échanges d’énergie ..................................................................................................................... 49
5.3 Quantification des niveaux d’énergie d’un atome, d’une molécule, d’un noyau ...................................................... 49
6 NOTATIONS, UNITES ET VALEURS ................................................................................................................................... 50
7 CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES................................................................................................................ 51

32
D Evolution temporelle des systèmes mécaniques
1 La mécanique de Newton
Le vecteur vitesse
Définissons rigoureusement le vecteur vitesse instantanée
Dans le repère (O,
1
e
,
2
e
,
3
e
) lié au référentiel d’étude, un point M est repéré par le vecteur position
3M2M1M e.ze.ye.xOM  
. Le point M est en mouvement par rapport au référentiel et donc
OM
est
une fonction du temps. L’utilisation du vecteur position
OM
permet d’écrire :
t
OM
vM
(cf. cours 1ère S)
t
OM
représente la vitesse pour un intervalle de temps t petit. Le passage à la limite nous permet de
définir la vitesse instantanée :
dt
OMd
t
OM
limv 0tM 
Le vecteur vitesse instantanée est donc la dérivée par rapport au temps du vecteur position
OM
.
Le vecteur vitesse instantanée a les caractéristiques suivantes :
- direction : la tangente à la trajectoire au point occupé par M à la date t
- sens : celui du mouvement à cet instant
- norme : la valeur positive
MM vv 
Les coordonnées du vecteur vitesse dans le repère (O,
1
e
,
2
e
,
3
e
) sont :
321321M e.ze.ye.xe
dt
dz
e
dt
dy
e
dt
dx
v
Deuxième loi de Newton (aspect semi quantitatif)
Un rappel du cours de 1S
Dans un référentiel galiléen, si le vecteur vitesse du centre d'inertie varie, la somme des forces qui
s'exercent sur le solide n'est pas nulle.
La variation, entre deux instants, du vecteur vitesse et la résultante des forces, appliquées entre ces deux
instants, ont la même direction et le même sens :
 Gext v )solide(F 
(cf. cours 1ère S)
Accélération du centre d’inertie
Définissons rigoureusement l'accélération
On filme le lancer d’une bille dans l’air. A l’aide d’un logiciel, on pointe sur chaque image la position du
centre de la bille. L’échelle étant définie, le logiciel calcule les vitesses instantanées et dessine les
vecteurs correspondants.

33
Le poids est la seule force qui s’exerce sur la bille :
PFext
. On constate sur la figure ci-dessus que
les vecteurs
P
et les
G
v
ont même direction, même sens et des valeurs proportionnelles :
 Gext vFP 
.
Les mesures étant réalisées sur un même intervalle de temps t, on en déduit que
ext
F
et
t
vG
sont
également proportionnels :
t
v
FG
ext
t
vG
caractérise l’accroissement de la vitesse (ou accélération) pour un intervalle de temps t petit. Le
passage à la limite nous permet de définir l’accélération instantanée :
dt
vd
t
v
lima GG
0tG
Le vecteur accélération instantanée est la dérivée par rapport au temps du vecteur vitesse.
Le vecteur accélération instantanée a les caractéristiques suivantes :
- direction et sens : vers l’intérieur de la concavité de la trajectoire
- norme : la valeur positive
GG a a 
Dans un repère ( O,
1
e
,
2
e
,
3
e
), les coordonnées du vecteur accélération sont :
3213z2y1x3
z
2
y
1
xe.ze.ye.xe.ve.ve.ve
dt
dv
e
dt
dv
e
dt
dv
a
Le repère de Frenet
Un repère privilégié pour étudier les mouvements curviligne et circulaire
La courbe décrite par un point est appelée trajectoire de ce point dans le référentiel d’étude. s est
l’abscisse curviligne c’est-à-dire la distance orientée parcourue par M sur sa trajectoire.
On montre mathématique que
T
dt
ds
v 
et
N
R
v²
T
dt²
d²s
a 
T
est le vecteur unitaire tangent à la trajectoire.
N
est le vecteur unitaire normal à la trajectoire et R le
rayon de courbure de cette trajectoire au point considéré.
3G4G vv  
1G2G vv  
1
2
3
4
5
6
7
8
1
3
5
7
8
5G6G vv  
7G8G vv  

34
Il est alors commode de définir le trièdre (
T
,
N
,
erP
) de Frenet, un repère mobile lié au mouvement du
point, dans lequel
erP
est le vecteur unitaire perpendiculaire au plan (
T
,
N
). Dans ce repère :
 les composantes de la vitesse dans le repère de Frenet
0 0, ,vT
=
0 0, ,
dt
ds
 les composantes de l’accélération dans ce repère
0,a,a NT
=
0 ,
R
v²
,
dt
dv
=
0 ,
R
v²
,
dt²
d²s
Il faut bien comprendre que la vitesse ci-dessus n’est pas celle « par rapport au repère de Frenet ». En
effet celle-ci serait nulle puisque ce repère suit le point dans son mouvement. La vitesse
v
n’est définie
que par rapport à un référentiel. Une fois ce vecteur défini, par rapport à un référentiel, on peut exprimer
les composantes dans n’importe quel repère géométrique ; celui-ci, contrairement au référentiel,
n’intervient pas dans la définition du mouvement.
Première loi de Newton
Un rappel du cours de 1S
Le centre d'inertie d'un solide isolé ou pseudo isolé est soit au repos soit animé d'un mouvement rectiligne
uniforme par rapport aux référentiels galiléens (et réciproquement).
nstCou 0v 0)solide(F Gext
(cf. cours 1ère S)
Le PCI ne concerne que le centre d'inertie du système. Ce qui n'exclut pas la rotation éventuelle du
système autour de son centre d'inertie.
Rôle de la masse
Une définition « expérimentale » de la masse pour introduire la deuxième loi de Newton
T
N
R
trajectoire
cercle osculateur
ext
5G6GG FP
t
vv
t
v
1
3
5
7
8
sens de parcours de la trajectoire

35
Dans l'expérience précédente on constate que le rapport
G
ext
a
F
est très voisin de la masse m du solide. La
masse joue le rôle de « coefficient d'inertie » : avec une même force appliquée à deux objets,
l'accélération est d'autant plus grande que la masse de l'objet est faible.
Deuxième loi de Newton appliquée au centre d'inertie
Dans un référentiel galiléen, la somme des forces extérieures
ext
F
appliquées à un solide est égale au
produit de la masse m du solide par l'accélération
G
a
de son centre d'inertie :
Gext a.mF 
Référentiels galiléens
Des référentiels privilégiés dans lesquelles le mouvement d'un point isolé est rectiligne et uniforme
En cherchant à vérifier expérimentalement la deuxième loi de Newton, on arrive à la conclusion que le
référentiel héliocentrique est galiléen et qu'il existe une infinité de référentiels galiléens, tous animés par
rapport au référentiel héliocentrique d'un mouvement de translation rectiligne uniforme.
Les référentiels terrestre et géocentrique ne sont pas galiléens puisque la Terre tourne autour du soleil.
Néanmoins, pour la plupart des applications pratiques qui ne réclament pas une extrême précision,
l'expérience montre qu'ils peuvent être considérés comme galiléens.
Troisième loi de Newton : loi des actions réciproques
Un rappel du cours de 1S
Les indications des dynamomètres A et B sont identiques. Les forces
ABBA Fet F 
ont même intensité,
même direction et des sens contraires
ABBA F- = F 
(cf. cours 1ère S)
Ce résultat s'applique à toute interaction entre deux systèmes, qu'ils soient en mouvement ou immobiles,
qu'ils soient en contact ou non.
2 Etude de cas
2.1 Chute verticale d’un solide
Champ de pesanteur
Nous aurons à utiliser ces notions par la suite
La célèbre « expérience par la pensée » d’Einstein suggère que le champ de pesanteur
g
de la Terre est
localement équivalent à une accélération
a
:
A B
F
B A
F
A
B