Utilisation du logiciel Radiochronologie

1
La radiochronologie : détermination d’âges absolus à l’aide de la radioactivité.
Utilisation d’un logiciel dédié en Tale S.
La radiochronologie est la méthode de datation absolue la plus utilisée en géologie.
1 - Principe de la radiochronologie
Un isotope radioactif «élément père » se transforme progressivement en isotope
radiogénique ou « élément fils » suivant la loi de décroissance radioactive
1
:
N(t) = N0 . e-t (voir l’annexe 1 pour les conditions de validité de la formule)
avec N(t) : nombre d’atomes de l’isotope radioactif à l’instant t, N0 : nombre d’atomes de
l’isotope radioactif à l’instant 0 et  : constante de radioactivité de l’isotope radioactif
étudié.
La loi de décroissance radioactive permet de connaître le temps t à condition de pouvoir
déterminer Nt , ce qui est assez facile avec un spectrographe de masse (ou des techniques
plus récentes) et N0, ce qui est plus difficile. t = ln(N0/N(t)) /  .
Quel temps mesure-t-on ? (Quel est le zéro du N0 ?)
La détermination de N0 se fait de manière plus ou moins complexe suivant les cas, à
partir du dosage d’éléments fils dans la roche (sauf dans certains cas (14C ...)). On date
alors le temps depuis lequel la roche n’échange plus ni isotope radiogénique ni élément
radioactif avec ce qui l’entoure. L’arrêt des échanges est ce que l’on appelle la
« fermeture du système » formé par la roche. Pour une lave, ce sera le moment de
refroidissement brutal de la lave, qui fige la roche et empêche ensuite les échanges
2
etc...
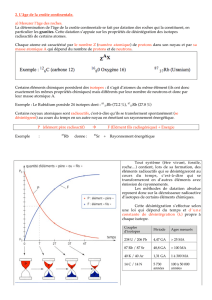
La période T (ou demi-vie) de l’élément radioactif est le temps au bout duquel la quantité
d’élément radioactif est divisée par deux : NT = N0 / 2 et donc T = ln 2 /  .
Principaux couples
d’isotopes utilisés
Constante de
radioactivité (an-1)
Période (années)
Domaine de datation
238U  206Pb
1,55125 x 10-10
4,47 x 109
235U  207Pb
9,8485 x 10-10
0,704 x 109
plus de 25 Ma
232Th  208Pb
4,9475 x 10-11
14,0 x 109
40K  40Ar 3
5,81 x 10-11
11,9x 109
1 à 300 Ma
87Rb  87Sr
1,42 x 10-11
48,8 x 109
plus de 100 Ma
14C  14N
1,245 x 10-4
5,730 x 103
100 à 50 000 ans
Constantes et domaines d’utilisation des principaux couples d’isotopes utilisés en radiochronologie.
Pour les datations, on ne pourra utiliser que des radio-isotopes présents dans la roche
étudiée et dont la période est du même ordre de grandeur que le temps que l’on veut
mesurer. Ainsi, on ne peut utiliser le 14C pour dater des objets plus anciens que 50 000 (ou
parfois 100 000 ans).
2 – Quelques exemples illustrés avec le logiciel
Le logiciel radiochronologie présente un modèle de décroissance de la quantité
d’éléments radioactifs et donne des exemples de datation en rapport avec le programme de
Tale S.
4
1
La loi fondamentale, plus facile à comprendre est celle qui concerne la vitesse d’apparition du produit (voir
Annexe 1)
2
Si tant est qu’un réchauffement propice au métamorphisme ne facilite pas la diffusion des éléments.
3
La période (demi-vie) indiquée ne correspond pas à grand chose. Le 40K se désintègre aussi en 40Ca (voir 2.3)

2
2 . 1 - Loi de décroissance.
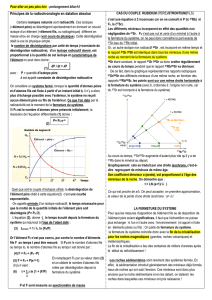
Cette partie du logiciel présente une simulation qui permet d’explorer la vitesse de
décroissance des éléments. On peut rechercher la période (temps au bout duquel le
rapport N / N0 = ½ ) et vérifier que la valeur ¼ est atteinte après une nouvelle période...
On peut choisir l’isotope radioactif servant de support au modèle et montrer ainsi, par
comparaison, que les datations ne sont envisageables que pour des durées en rapport avec
la période de l’isotope considéré (comparer 238U, par exemple, et 14C).
Cinq isotopes ont été choisis dans le logiciel : 238U, 235U, 40K, 14C et 87Sr.
Les isotopes 238 et 235 de l’uranium sont à l’origine de familles radioactives
complexes qui aboutissent respectivement aux isotopes 206 et 207 du plomb. On peut
négliger les éléments intermédiaires de ces familles dans la mesure où la période de
désintégration des éléments qui la compose est au moins 10 000 fois plus courte que celle
de l’élément de départ. Tout se passe donc pratiquement comme si la transformation était
directe.
Pour la désintégration du 40K, le logiciel contient 2 modèles dans le menu loi :
 Le modèle simpliste ne tient compte que de la transformation 40K 40Ca. Les
résultats affichés sont donc purement théoriques et ne correspondent pas ni à la
réalité de l’évolution du nombre d’atomes de 40K ni à celle d’apparition de 40Ar
(car celle-ci suit une loi plus complexe – voir Annexe 2).
 Le modèle plus réaliste tient compte des deux transformations.
2 . 2 - Datation d’un morceau de bois avec le 14C :
L'isotope 14 de l'élément Carbone (14C) est produit en permanence dans la haute
atmosphère à partir de l'isotope 14 de l'élément Azote (14N), sous l'effet des rayons
cosmiques.
Comme cette production compense la perte par radioactivité, le rapport isotopique
14C / 12C reste donc constant pour le CO2 de l'atmosphère. Ce rapport isotopique reste
donc aussi constant dans les tissus vivants qui incorporent le CO2, directement (cas des
végétaux autotrophes) ou non (cas des hétérotrophes).
Après la mort, le 14C n'est pas renouvelé et le rapport isotopique décroît suivant la loi
de décroissance radioactive. L'âge de l'échantillon est calculé à partir de la mesure de sa
radioactivité exprimée en coups par minutes et par gramme de carbone. Aujourd’hui, la
radioactivité du carbone des tissus vivants est de 13,56 cpm/g.
Pour déterminer l'âge d'un fragment de bois retrouvé dans une coulée de laves et dont
la radioactivité est de 8,56 cpm/g , il suffit d’appliquer la loi de décroissance de la
radioactivité, ce qui est simplifié par l’utilisation du logiciel.
L'âge ainsi estimé doit être corrigé pour tenir compte des variations de la teneur en
CO2 de l'atmosphère qui ont fait varier le rapport isotopique 14C / 12C.
2 . 3 - Datation de roches par la méthode K - Ar :
Le 40K se transforme en 40Ar par capture d’un électron. La demi-vie très longue de
cette transformation (12,9 Ga – constante λK = 0,581.10-10 an-1) permet d’utiliser cette
méthode pour des roches très anciennes. Dans ce cas, c’est la quantité d’élément
radiogénique qui peut être connue dans des circonstances favorables.
Dans les roches magmatiques, les gaz comme l’argon remontent vers la surface de la
masse en fusion. La quantité d’argon est donc nulle au sein de la roche au moment de sa
4
La version datée « Novembre 2001 » du document d’accompagnement du programme comporte quelques
coquilles : la demi-vie du 14C est de 5730 ans (et non 5370). La demi-vie du 87Rb est de ≈ 50 milliards d’années
(et non 50 millions).

3
solidification. Si la roche (ou le minéral) ne laisse pas diffuser ce gaz
5
, tout l’argon que
l’on peut extraire de la roche provient de la transformation du 40K. La méthode demande
un très grand soin pour éviter les contaminations par l’atmosphère qui est relativement
riche en Ar (environ 1%). Il faut préchauffer l’échantillon pour détacher les molécules
adsorbées à sa surface, puis le faire fondre dans une enceinte au vide très poussé. La
mesure de la quantité d’Ar se fait au spectrographe de masse sous ultravide.
Attention ! La relation entre la quantité d’Ar et le temps n’est pas celle que l’on
pourrait déduire de la formule classique. Le 40K se transforme aussi en 40Ca avec une
émission β. La période est alors un peu plus courte (1,4 Ga – constante λβ = 4,962.10-10
an-1) Au total, la disparition du 40K se fait avec une demi-vie de 1,25 Ga.
Le temps t se calcule avec
K
Ar
Lnt
K
K
K40
40
1
1
(voir Annexe 2 pour
la démonstration).
soit
 K
Ar
Lnt40
40
10 5404,9110.1804,0
où t est exprimé en années.
Le logiciel permet de suivre l’évolution du rapport 40Ar/40K au cours du temps et
permet ainsi une datation à partie de valeurs concernant telle ou telle roche.
Remarques :
 La méthode est limitée dans le temps par la vitesse de diffusion de l’argon.
 L’isotope 40 du Ca étant le plus commun, il est rare de pouvoir l’utiliser comme
on peut le faire pour l’argon.
Application : (d’après B. Chopineaux et J-P. Debenay – Exercices de Géologie) :
Un dosage effectué sur un basalte fournit 3,311.10-3 µg de 40Ar pour 6,140 µg de 40K.
Quel est son âge ?
2 . 4 - Datation de roches par la méthode Rb - Sr (d’après le document d’accompagnement du
programme de TS)
Le rubidium est un élément souvent associé au potassium (situé juste au-dessus dans le
tableau de Mendeléiev). Son isotope 87 (87Rb) qui est radioactif se désintègre en
strontium 87Sr avec une émission β. Le Strontium est lui plutôt associé au calcium. La
demi-vie est de 48,8 milliards d’années.
Ce cas (qui correspond à un cas plus général de datation) est plus complexe que les
deux précédents. Il s’agit de trouver l’âge de la roche alors que les quantités initiales
d’isotope père et d’isotope fils sont inconnues. Pour cela, il faut des mesures provenant
d’au moins deux échantillons de même origine. L’utilisation d’un isotope de référence est
alors indispensable pour comparer les mesure des différents échantillons. C’est l’isotope
86Sr qui est stable (comme 87Sr) mais qui n’est pas radiogénique qui a ici ce rôle.
La loi de décroissance radioactive a ici sa forme habituelle :
NRb(t) = NRb0 e-λ
t [1]
où NRb(t) représente le nombre d’atomes de 87Rb au temps t et NRb0 le nombre initial.
Si les échantillons ont une même origine et n’ont échangé ni Sr ni Rb avec l’extérieur,
les points représentant les échantillons dans un repère d’abscisse 87Rb/86Sr et d’ordonnée
87Sr/86Sr sont alignés et la pente (A) de la droite est reliée au temps par la formule :
A = eλt-1 d’où on tire
)1ln( 
A t
voir le détail du calcul dans l’annexe 3.
5
Les micas et les hornblendes, par exemple, retiennent bien l’Ar alors que les feldspaths potassiques le laissent
échapper.

4
Application : (d’après J-M. Caron, A Gauthier, A. Schaaf, J. Ulysse, J. Wozniak –
Comprendre et enseigner la planète Terre) :
Des dosages effectués sur 9 échantillons de granodiorites et de granite de Plouaret
(Bretagne) ont donné les résultats suivants :
Echantillo
n
1
2
3
4
5
6
7
8
9
10
11
87Rb/86Sr
1,54
5,60
5,70
12,2
3,38
4,52
4,81
0,209
2,47
6,18
11,14
87Sr/86Sr
0,7129
0
± 9.10-
5
0,7324
7
± 6.10-
5
0,7324
7
± 6.10-
5
0,76367
± 11.10-
5
0,7228
9
± 9.10-
5
0 ,726
66
± 7.10-
5
0,7278
2
± 7.10-
5
0,7066
4
± 9.10-
5
0,7167
1
± 7.10-
5
0,7340
8
± 8.10-
5
0,7109
9
± 7.10-
5
Les conditions nécessaires à la détermination de l’âge sont-elles réunies ? quel est l’âge des
roches donné par la méthode ? A quel événement correspond-il ?
Un autre exemple concernant la datation de coulées de laves du « grand Canyon » montre
les limites de ces méthodes :
Données concernant les laves de Cardenas à l’Est du grand canyon qui sont profondément
enfouies : âge K-Ar compris entre 760 et 860.106 ans
Echantillon
1
2
3
4
5
6
87Rb/86Sr
1,133
1,305
1,597
1,677
2,288
2,673
87Sr/86Sr
0,72436
0,72756
0,73077
0,73045
0,74263
0,74727
Données concernant la coulée de laves de l’Ouest du grand canyon qui est en surface et a
un aspect récent : âge K-Ar 1,2 ± 0,2.106 ans
Echantillon
1
2
3
4
5
6
87Rb/86Sr
0,0544
0,0667
0,0860
0,1193
0,1211
0,2193
87Sr/86Sr
0,70325
0,7043
0,7037
0,705
0,7046
0,7069
2 . 5 - Datation de la nucléosynthèse de l’élément Uranium du système solaire :
(d’après Ph. Vidal – Géochimie)
Données : Les expériences de collision dans des accélérateurs de particules ont permis
de montrer que lorsque l’élément U se forme par fusion de noyaux, comme dans
certaines étoiles, le rapport des quantités d’isotopes est de 238U/235U = 1,505. Des
mesures effectuées sur des roches terrestres, des roches lunaires et des météorites ont
montré que le rapport moyen de ces deux isotopes dans le système solaire est aujourd’hui
de 137,8. A partir de ces données, il est possible de calculer le temps moyen écoulé
depuis la nucléosynthèse de l’élément Uranium. Le logiciel présente une simulation de
l’évolution du rapport isotopique à partir de l’instant de la nucléosynthèse pris comme
temps t = 0.
Le modèle mathématique est assez simple dans ce cas :
238
235
238
235 1505
U
UU Ue e
t t
(). .
, .
  8,29725.10-10
Question : Quel est l’âge moyen de l’élément U du système solaire ?
On observera, après la datation suivante, que cet élément est plus ancien que le
système solaire lui-même. Le soleil, étoile qui ne synthétise pas de noyaux lourds comme
ceux d’uranium est donc une étoile de deuxième génération au moins. Dans ce cas, la
référence de temps est fournie par les conditions initiales qui ont été établies par une
t
0

5
méthode indépendante. Le « système clos » est l’ensemble du système solaire et la
nébuleuse qui lui a donné naissance.
Remarque : pour simplifier, le modèle dessiné ne tient pas compte du plomb initial.
Cet élément n’intervient pas dans le calcul.
2 . 6 - Datation du système solaire : (d’après C. Allègre : De la Pierre à l’étoile)
Principe : La désintégration des isotopes 238 et 235 de l’élément Uranium donne
respectivement naissance aux isotopes 206 et 207 de l’élément Pb. En estimant les
quantités d’isotopes 206Pb et 207Pb issus de la désintégration radioactive de l’Uranium, on
peut estimer le temps écoulé depuis que ces isotopes sont produits dans une roche.
Deux problèmes compliquent les calculs :
Il y a une quantité initiale de Pb, inconnue, variable selon la roche, et qui s’ajoute à
la quantité d’origine radiogénique. L’étude de minéraux issus de météorites riches en
Pb et très pauvres en U (sulfure de canyon diablo) permet de s’affranchir de ce
problème : les rapports isotopiques du plomb y sont restés inchangés.
Plus la roche contient d’uranium, plus vite elle s’enrichit en plomb d’origine
radiogénique. Cette inconnue est éliminée en utilisant en même temps les
renseignements issus de la désintégration radioactive des deux isotopes.
Pour pouvoir comparer entre elles les différentes roches nécessaires à l’étude, on
rapporte les quantités de 207Pb et de 206Pb à la quantité d’isotope 204Pb. Cet isotope du
plomb n’est ni radiogénique ni radioactif, sa quantité est donc stable et peut servir de
référence.
On choisit des roches provenant de milieux que l’on peut considérer comme clos et
assez homogènes depuis la formation du système solaire. Il s’agit de roches issues de
météorites de roches lunaires et d’un basalte de point chaud (qui vient des profondeurs du
manteau terrestre qui est brassé par des mouvements de convection).
Les données sont rapportées sur un graphique :
Détermination de l'âge du système solaire
0
20
40
60
80
100
120
140
160
180
200
050 100 150 200 250 300
La pente du géochrone est égale à 0,618.
Les données correspondant aux différentes roches sont alignées ce qui s’explique par le
fait qu’elles sont toutes représentatives de milieu clos de même âge : l’âge du système
solaire (voir les calculs). On suppose que les planètes et météorites se sont formées toutes
en même temps, tout au début du système solaire. La droite reliant les coordonnées des
différentes roches est appelée le géochrone. La mesure de sa pente permet de calculer le
temps depuis que les systèmes considérés sont clos : l’âge du système solaire.
La partie gauche de l’écran du logiciel schématise l’évolution de la teneur en différents
isotopes d’uranium et de plomb pour quatre roches théoriques de compositions initiales
variées.
207Pb/204Pb
206Pb/204Pb
Roche
lunaire
Sulfure de
Canyon Diablo
Météorite de
Nuevo Latedo
Basalte de Hawaï
géochrone