Principes de radiochronologie

RR - 17/04/17 - 582667781 - 1/1
Principes de radiochronologie
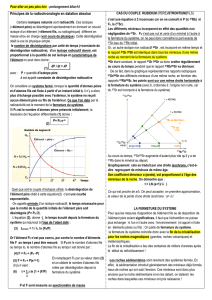
● Un isotope "père" P radioactif, se désintègre
spontanément en un isotope "fils" F radiogénique,
selon une fonction exponentielle du temps.
P = P0 e-
t donc
P
P
ln
1
t0
λ
[1]
P = quantité d'isotope père actuelle
P0 = quantité d'isotope père initiale
F = quantité d'isotope fils actuelle
F0 = quantité d'isotope fils initiale
= constante de désintégration
t = durée de désintégration
Démonstration. La quantité d'atomes radioactif dP disparaissant
par désintégration pendant un intervalle de temps dt est telle que
dP/dt = - P0 qui, après intégration, donne P = P0 e-
t
On en tire P0 / P = 1 / e-
t = e t d'où
t = ln P0 / P
(ln = logarithme népérien), donc t = 1/ . ln P0 / P
● En général P0 est inconnu mais F est mesurable. On a
alors :
F = F0 + P. t donc
λ P FF
t0
[2]
Démonstration. La quantité F d'isotope fils actuelle est égale à la
quantité initiale F0 plus la quantité formée par désintégration Fd,
soit : F = F0 +Fd.
Or Fd est égal à la quantité d'isotope père désintégré (un atome
de P donne un atome de Fd), on a donc :
Fd = P0 - P d'où : F = F0 + (P0 - P)
Puisque d'après [1] P0 = P e
t on peut écrire F = F0 + ( P e t - P)
soit F = F0 + P (e
t - 1)
- Or e
t -1
t cette approximation est très pratique et on peut à
tout moment revenir à l'expression initiale.
On a donc F = F0 + P. t et t = F - F0 / P
- On peut aussi choisir de "traîner" e
t -1.
Puisque F = Fo + P (e
t - 1) on a F - F0 = Pe t - P donc F-F0 / P
= e
t - 1 et F - F0 + 1 = e t d'où on tire t = 1/
ln (F - F0 / P + 1).
1. Cas du carbone 14
● 14C (élément père) est un isotope radioactif qui se
désintègre en 14N (élément fils).
En système ouvert 14C est constamment renouvelé, de
sorte que 14C / 12C = 1,2 . 10-12 = constante
T du 14C = 5 730 ans et = 1,209. 10-4. an-1
Puisque P0 est connu, l'expression [1] peut être
directement utilisée.
14C = 14C0 e- t donc
C
C
ln
1
t14
0
14
λ
Puisque la quantité de 12C est constante (ni radioactif ni
radiogénique), on peut aussi écrire :
14C / 12C = (14C / 12C) 0 . e- t
2. Cas du couple K/Ar
● Le 40K (élément père) est un isotope radioactif dont
10,5% des atomes se désintègrent en 40Ar (élément
fils). T = 1,25.109 ans et
= 5,54.10-10. an-1
La quantité initiale 40K0 est inconnue, l'expression
[1] est donc inutilisable. On utilise donc l'expression
[2] en considérant que F0 = 40Ar0 = 0 (négligeable).
40Ar = 0,105 40K.
t d'où on tire
λK0,105 Ar
t40
40
- On peut aussi écrire : 40Ar / 40K = 0,105 t
ou 40Ar / 40K = 0,105 e
t - 1 (car on a vu que
t ≈ e
t -1)
- Si on calcule t sans approximation on a vu que
t = 1/ . ln (F / P + 1) donc t = 1/  . ln (40Ar / 0,105 40K + 1)
3. Cas du couple Rb/Sr
● Le 87Rb (élément père) est un isotope radioactif qui
se désintègre en 87Sr (élément fils). Le 86Sr est un
isotope stable.
T = 48,8.109 ans (≈ 50.109 ans) et = 1,42.10-11. an-1
87Rb0 est inconnu on applique donc l'expression [2].
87Sr = 87Sr0 + 87Rb.
t
● Cette équation a deux inconnues : 87Sr0 et t.
On doit donc disposer de deux équations, ce qui impose de
travailler sur deux minéraux de la même roche (qui ont donc le
même âge). Or, dans les deux minéraux, les quantités initiales
des isotopes impliqués sont différentes car leurs compostions
chimiques sont différentes. Pour éviter ce problème on mesure
des rapports isotopiques qui eux sont identiques (mais
inconnus) à l'origine. Pour cela on divise les deux membres de
l'équation ci-dessus par 86Sr qui est stable donc connu (ni
radioactif ni radiogénique).
On obtient une équation de la forme : y = Ax + B
Sr
Sr
86
87
= t .
Sr
Rb
86
87
+
Sr
Sr
86 0
87
avec pour inconnues A = coefficient directeur de la
droite ( t ≈ e
t -1) et B = valeur de y à l'origine.
● On utilise alors une méthode graphique qui consiste
à mesurer les rapports isotopiques 87Sr/86Sr et 87Rb/86Sr
d'au moins deux minéraux différents de la même roche.
En reportant ces points sur un graphique y = 87Sr / 86Sr
en fonction de x = 87Rb / 86Sr (= droite isochrone) on
détermine graphiquement l'ordonnée à l'origine
(87Sr0/86Sr0 = 87Sr0/86Sr car 86Sr est constant). Cela
permet d'estimer 87Sr0.
Le coefficient directeur de la droite isochrone augmente
au cours du temps. Il est nul à t = 0. Lorsque le temps
s'écoule la droite pivote autour de l'ordonnée à l'origine,
qui demeure fixe. Si l'on choisit les mêmes unités en
abscisse et en ordonnée, les points représentatifs des
différents échantillons décrivent des segments de droite à
45°, car à chaque fois qu'un noyau de 87Rb se désintègre,
il apparaît un noyau de 86Sr.
Deux minéraux suffisent pour tracer la droite. Mais trois
permettent de vérifier que c’est une droite.
● Il ne reste plus qu'une inconnue : l'âge de la roche
qui est déduit du coefficient directeur de la droite ( t ≈
e
t -1). Plus ce coefficient directeur est fort, plus les
échantillons sont vieux.
A = t donc
λ
A
t
Sans approximation, on rappelle t ≈ e
t -1,
A = e
t -1 d’où on tire t = ln (A+1) /