Chapitre 8 eleve 2012

Chapitre 8
Techniques de datation en géologie
Au début du XIXème siècle, une longue durée des phénomènes géologiques et de l’histoire de la
Terre est acceptée. Charles Lyell (1797-1875) est partisan d’un temps « infini ». Lord Kelvin (1824-1907)
calcule un temps de 20 à 40 MA pour que la variation de température près de la surface (le gradient
géothermique) atteigne la valeur actuelle de 37°C/km. Il défend un âge fini de la Terre estimé à 100 MA.
La découverte de la radioactivité par Henri Becquerel (1852-1908) en 1896 va permettre en 1953 de
dater les météorites et d’estimer l’âge de la Terre à 4,55 milliards d’années (valeur acceptée depuis
1970).
I la datation relative
A les principes de la datation relative
La datation relative permet d’ordonner des structures géologiques (strates _synonyme de
couche_, plis, failles, minéraux) les unes par rapport aux autres, ainsi que des événements géologiques
variés (discordance, sédimentation, intrusion, orogenèse). Elle repose sur les principes de la chronologie
relative :
Principe d’actualisme : aux mêmes cause les mêmes effets, quelle que soit l’époque
Principe de continuité : une même couche a le même âge sur toute son étendue.
Principe de superposition : de deux couches superposées, non renversées par la tectonique, la plus
basse est la plus ancienne.
Principe de recoupement : il permet de traiter toutes les situations d’intersection entre couches ou
formations. Par exemple, pour une déformation : l’événement ayant généré les changements de géométrie
des couches est postérieur à la formation qu’il affecte.
Principe d’identité paléontologique : l’identification dans une couche de fossiles dits stratigraphiques
permet d’affecter à la couche le même âge qu’une autre couche d’âge connu contenant les mêmes fossiles.
Un bon fossile stratigraphique vit peu longtemps, partout sur la planète.
B Conséquence : l’échelle stratigraphique des temps géologiques
L’utilisation de ces principes a permis de construire une référence temporelle qui a une valeur
générale et s’applique à toutes les études géologiques : l’échelle stratigraphique internationale des
temps géologiques.
II la datation absolue ou chronologie absolue
La chronologie absolue, en donnant accès à l'âge des roches et des fossiles, permet de mesurer
les durées des phénomènes géologiques. Elle permet aussi de situer dans le temps l'échelle relative des
temps géologiques.
A Les principes généraux d’application de la datation absolue
La chronologie absolue est fondée sur la décroissance de la quantité d’isotopes radioactifs de
certains éléments chimiques : elle exploite la relation qui existe entre le rapport isotopique et la durée
écoulée depuis la « fermeture du système » contenant les isotopes.
Les isotopes d’un élément possèdent le même nombre d’électrons et de protons, mais un nombre
de neutrons différent. Certains isotopes sont stables (
12
C,
13
C) d’autres radioactifs (
14
C). Dans ce cas,
leur noyau peut se transformer en un autre noyau en perdant une particule et en émettant un type de
rayonnement. Ceci se fait selon la loi de désintégration radioactive :

dN/dt = - λ
λ λ
λN où λ
λλ
λ est la constante de désintégration
⇨dN/N = - λdt
⇨ ln N = - λt+C
⇨ N = e
-λt+C
⇨ N = e
-λt
e
C
Or à t = 0, N = N
0
= e
0
e
C
donc N = e
-λt
N
0
⇨ ln (N/ N
0
) = λt
t = ln(N
0
/N) / λ
λλ
λ
La faisabilité et la qualité de la datation dépendent de :
1 La période de l’isotope choisi pour l’analyse
On appelle période ou demi-vie le temps nécessaire pour que la moitié des noyaux radiogéniques se
désintègrent.
No/N = 2 donc
t
1/2
= 1/λ ln 2
Une fois le système fermé, la quantité d’isotope susceptible de se désintégrer diminue. La
datation n’est valide que si l’on mesure des durées allant du centième à dix fois la période de l’isotope
choisi. Les radiochronomètres sont choisis en fonction de la période de temps que l’on cherche à
explorer.
2 La qualité et la pertinence de l’échantillon utilisé
La date calculée correspond à celle où les isotopes de l’échantillon utilisé (fraction minérale ou
roche totale) ont été confinés : aucun constituant n’a pu quitter l’échantillon et aucun des constituants
extérieurs n’a pu y entrer. A partir de cette date, les éléments chimiques ont évolué spontanément en
suivant les lois physiques de désintégration radioactive sans interaction avec le milieu. On parle de
système fermé.
Remarque : en général, les roches sédimentaires ne sont pas des systèmes fermés et sauf cas particulier
comme le carbone 14, la radiochronologie ne permet pas de dater les roches sédimentaires.
B trois exemples d’isotopes utilisés en SVT
Vous devez savoir les utiliser avec équations, constantes et courbes fournies dans l’exercice. Les
explications (à comprendre mais pas forcément à retenir sont en italique).
1 la datation au carbone 14
Du fait de sa demi-vie de 5730 ans, le carbone 14 est particulièrement bien adapté à la mesure de
durées de quelques dizaines de milliers d’années au plus (100 à 50 000 ans).
Cet isotope est produit régulièrement en haute atmosphère à partir de l’azote de l’air. Lorsqu’un animal ou
une plante meurt, son métabolisme cesse et son carbone n’est plus renouvelé ; les isotopes radioactifs se
désintègrent. Il en est de même pour un carbonate précipité et isolé ou une masse d’eau isolée. En connaissant la
proportion de
14
C/
12
C dans le milieu, la mesure de la proportion de
14
C/
12
C dans les restes d’êtres vivants (os,
cheveux, bois, coquilles) fournit la durée écoulée depuis la mort ou « isolement » (fermeture du système). Au-delà
de 30000 à 40000 ans, la quantité de carbone 14 restant dans l’échantillon est insuffisante pour permettre une
mesure fiable. Les appareils arrivent à mesurer des rapports de concentrations mais n’arrivent pas à mesurer des
concentrations simples…

On mesure r =
14
C/
12
C que l’on compare à r* rapport actuel supposé constant (il faut en fait faire
des correctifs). Alors
No/N = r*/r
avec λ =
λ = λ =
λ = 1,245 10
-4
ans
-1
et on en déduit t grâce à l’équation t = ln (N
0
/N) / λ
λλ
λ
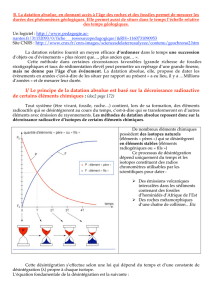
On peut également réaliser une détermination graphique de l’âge de l’échantillon
La courbe de désintégration du carbone 14
2 la datation par la méthode potassium/argon
Le couple Potassium/Argon permet d’aborder des datations de roches plus anciennes (1 à 300 Ma).
En pratique, on dispose du rapport
40
Ar/
40
K et on utilise une méthode de résolution graphique ou
numérique avec l’équation (fournie):
Résolution pour un rapport de 0,0053 : 90 MA
Contrairement au
14
C, il n’y a pas d’isotope radioactif au départ. Il est équivalent de mesurer des
rapports isotopiques exprimant le nombre d’isotopes disparus ou apparus.
La désintégration du
40
K n'est pas simple mais suit plusieurs voies qui sont schématisées dans la
figure ci-contre :
• Une voie mène au
40
Ca par désintégration β (plus de 88% de la désintégration du
40
K)
• Une autre voie, elle-même complexe, mène au
40
Ar, essentiellement par capture électronique (EC).
Il faut tenir compte dans les formules de calcul du temps de ces deux voies de désintégration, en
utilisant une constante de désintégration totale, égale à 5,543.10
-10
an
-1
.
Remarque : cette méthode suggère l’existence de limites à la datation absolue. L’isotope de l’argon existe
en quantité non négligeable dans l’atmosphère et les fluides circulants, l’échantillon daté peut-être
contaminé et conduire à des datations erronées (circulation de fluides, métamorphisme…).

3 la datation par la méthode rubidium/strontium
Cette méthode de datation est la plus courante. Elle utilise un couple d’isotopes dont la quantité
initiale est inconnue. Il y a donc deux inconnues : l’âge de l’échantillon et la quantité initiale d’isotope. Il
faut donc disposer d’au moins deux équations.
On effectue une mesure sur deux constituants
équivalents du même échantillon (minéraux).
87
Rb ------>
87
Sr + β
demi-vie = 48.8 milliards d'années, λ= 1.42 10
-11
an
-1
Pour résoudre ce problème, il faut comprendre qu’on ne peut mesurer que des rapports de
concentrations et que la cristallisation est un processus géologique qui ne fractionne pas les isotopes
d'un même élément lourd. Ainsi, deux minéraux ou deux roches cristallisant à partir d'un même magma
intégreront dans leur réseau cristallin du strontium (Sr) avec un rapport isotopique
87
Sr/
86
Sr identique à
celui du magma d'origine. On dit que ces échantillons sont cogénétiques. Et même si certains minéraux
intégreront plus de strontium que d'autres, tous auront le même rapport initial
87
Sro/
86
Sro. Par ailleurs,
sachant que
86
Sr n'est ni radioactif ni radiogénique, la quantité de cet isotope ne varie pas au cours du
temps dans un système clos et
86
Sr =
86
Sr
0
.
On peut mesurer les rapports
87
Sr/
86
Sr et
87
Rb/
86
Sr par spectrométrie de masse.
Si on divise toute l’équation par le nombre d’
86
Sr, l’équation devient donc :
C’est l’équation d’une droite dite isochrone : y = ax + b avec :
a = , b déterminé graphiquement, en ordonnée et en abscisse
La pente de la droite (tracée à partir d’au moins deux mesures) est déterminée graphiquement ce
qui permet de déduire le temps. Il faut que tous les points soient sur la même droite pour qu’ils
proviennent du même magma initial (même rapport
87
Sro/
86
Sr).