Inductance - NTE Lyon 1

Cliquer sur « affichage » puis « plein écran »
1
Inductance propre
1 - Données essentielles
Une bobine est un réservoir temporaire d’énergie sous forme magnétique. Elle se
compose d’un bobinage conducteur et d’un noyau magnétique qu’elle enlace.
L’énergie est stockée uniquement dans le matériau magnétique qui peut être aussi
simplement de l’air. Le métal du conducteur ne peut pas stocker d’énergie, mais par
sa nature bobiné en spires, il engendre un flux magnétique. Le flux magnétique  est
proportionnel au courant I qui passe dans les spires. Le coefficient de
proportionnalité L entre le flux  et le courant I est l’inductance propre. On confond
souvent le composant (bobine) avec la grandeur qui la caractérise (inductance).
Quand il n’y pas d’ambiguité on omet le qualificatif propre.
I.L
Unités : L en henry (L), I en ampère (A) et  en weber (Wb)
Symbole de l’inductance :
2 - Relation entre intensité et tension
Lorsque le courant dans les spires de la bobine varie, celle-ci devient siège d’une
f.e.m. d’auto- induction. Il existe une relation entre la tension et le courant, qui traduit
les propriétés électrocinétiques du composant bobine.
Par convention, la f.e.m. est de même sens que le courant.
A – Enoncé
dt)t(di
.L)t(u 
u(t)=-e(t)
e(t)
i(t)

Cliquer sur « affichage » puis « plein écran »
2
Unités : i en ampère (A), u en volt (V) et L en henry (L).
Remarque : Relation entre flux et tension :
)
dt
d
()t(e)t(u 
B – Conséquences
a) En régime continu, une inductance est un court-circuit
En régime continu, i=cte et donc u=0.
En fait, une bobine présente toujours une résistance propre, selon le schéma
équivalent suivant :
Une bobine est équivalente à une inductance « pure » en série avec une
résistance faible le plus souvent.
b) En régime périodique établi, la tension moyenne aux bornes d’une
inductance pure est nulle.
Au bout d’une période la tension reprend la même valeur : i(0)=i(T)
0Ldi
T
1
dt
dt
di
L
T
1
uU )T(i
)0(i
T
0
moyen0  
c) La tension ne peut être infinie, le courant i ne peut présenter de
discontinuité
d) Alimentation d’une bobine par un générateur de courant constant
Bilan énergétique :
Une bobine de résistance négligeable et d’inductance L, en parallèle sur une
conductance G est alimentée à l’instant t=0, par une source de courant constante I0 .
i(t)
t
Une situation physiquement impossible

Cliquer sur « affichage » puis « plein écran »
3
La bobine se charge en énergie magnétique. Elle a acquis le flux , en fin de charge.
L’énergie de la source de courant est convertie en énergie magnétique et en chaleur.
Un flux  est fourni par le générateur et il est stocké par la bobine (inductance
pure). A la fin de la charge, le courant dans la bobine est I0, car celle-ci est un court-
circuit.
Lors de la phase de charge de la bobine, le bilan d’énergie s’établit ainsi :
 La source perd I0.
En effet :
0
00 00IdIdt.u.I
 La bobine d’inductance pure gagne ½I0 .
En effet, l’énergie stockée par l’inductance est :
0
2
0
I
000 I
2
1
LI
2
1
di.Liiddt.i.u 0
 ½I0 est donc transformée en chaleur et considérée comme perdue.
On appelle Wem énergie magnétique ou énergie utilisable, l’énergie
convertible en travail électrique.
Pour une inductance supposée constante, parcourue par un courant I, l’énergie
utilisable est :
 I
2
1
LI
2
1
W2
em
Equations temporelles
On se place dans le cas général. Le courant dans l’inductance est i0 à l’instant
initial.
Equation différentielle régie par u :
dt
di
Lu
iGuI0
i
dt
di
LGI0
Solution particulière : i=I0
L
I0
G
u(t)
i(t)
(t)

Cliquer sur « affichage » puis « plein écran »
4
Solution générale de l’équation sans second membre :
)
LG
t
exp(Ki 
Conditions initiales : i(0)=i0.
Solution de l’équation :
)
t
exp(1(I)
t
exp(i)t(i 00 
La constante  est la constante de temps du système.
G.L
Unités :  en seconde, G en ohm-1 et L en henry.
Cas particuliers
Charge d’une condensateur à partir d’un état de totale décharge i0=0
)
t
exp(1(I)t(i 0
Décharge d’une bobine dans une conductance
)
t
exp(i)t(i 0
C - Exercice 1
Déterminer la puissance moyenne dissipée par effet Joule, dans l’exemple
précédent (on fera i0=0). On admet que le transitoire est quasiment terminé au bout
de 5.
Que vaut cette puissance si l’on fait G=0 ?
Conclure quant à la possibilité d’associer ainsi la source de courant parfaite et
la bobine d’inductance pure.
Pour la correction cliquer sur : correction
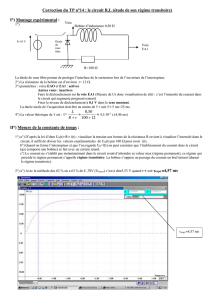
3 - Alimentation d’une composant RL (bobine réelle) par un générateur de
tension constante
Equations temporelles
On se place dans le cas général. Le courant dans l’inductance est i0 à l’instant
initial.

Cliquer sur « affichage » puis « plein écran »
5
Equation différentielle régie par i.
dt
di
Lu
uRiE
Ri
dt
di
LE 
Solution particulière : i=E/R
Solution générale de l’équation sans second membre :
)
Lt.R
exp(Ku 
Conditions initiales : i(0)=i0.
Solution de l’équation :
))
t
exp(1(
R
E
)
t
exp(i)t(i 0
La constante  est la constante de temps du système.
L
R
Unités :  en seconde, R en ohm et L en henry.
Cas particuliers
Charge d’une bobine à partir d’un état de totale décharge i0=0
))
t
exp(1(
R
E
)t(i 
Décharge d’une bobine dans une résistance
)
t
exp(i)t(i 0
Courbe de charge dans le cas particulier où i0=0 A
E
R
u(t)
i(t)
L