INTEGRATION

1/8
INTEGRATION
§ 1 Notion d’intégrale d’une fonction
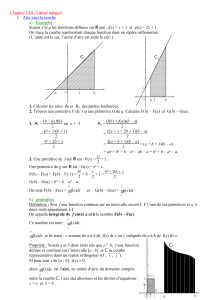
Le plan étant muni d'un repère orthogonal (O ;
i
,
j
) , on définit les points I, Jet K par
OI
=
i
,
OJ
=
j
et OIKJ rectangle.
L'aire du rectangle OIKJ définit alors l'unité d'aire (u.a.).
1. Aire et intégrale d'une fonction positive
Définition
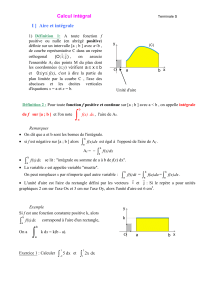
Soit f une fonction continue et positive sur un intervalle [a ; b] et C sa courbe représentative dans le
repère (O ;
i
,
j
)
L'intégrale de a à b de f est le réel noté
b
adx)x(f
, égal à l'aire, exprimée en unités d'aire, du domaine
D délimité par C, l'axe des abscisses et les droites d'équations x = a et x = b.
1. 2.
Remarque
a et b sont les bornes de l'intégrale et x est une variable muette :
elle n'intervient pas dans le résultat. On peut la remplacer par les lettres t ou
u, ainsi :
b
adx)x(f
=
b
adt)t(f
=
b
adu)u(f
Exemples
0
2dx3
= 6 D1 est un rectangle
3
1tdt
=
2)13(2 
= 4 D2 est un trapèze
2. Valeur moyenne
Définition
Soit f une fonction continue et positive sur un intervalle [a ; b] avec a < b. La valeur moyenne de f sur
[a ; b] est le réel μ =
b
adx)x(f
ab 1
μ =
b
adx)x(f
ab 1
équivaut à μ (b - a) =
b
adx)x(f
La valeur moyenne de f sur [a ; b] est donc le réel μ tel que le rectangle de dimensions μ et b - a soit de
même aire que le domaine D délimité par la courbe représentant f, l'axe des abscisses et les droites
d’équations x = a et x = b

2/8
§ 2 Intégrale et primitive
1. Intégrale d’une fonction continue, positive et croissante sur un intervalle [a ; b]
Théorème :
Soit f une fonction continue, positive et croissante sur un intervalle I = [a ; b] . On note C, sa courbe
représentative dans le plan muni d'un repère orthogonal.
On définit sur [a; b] la fonction A : x
x
adt)t(f
et on fixe x0 dans [a ; b]
la fonction A est dérivable sur I et sa dérivée est f
Démonstration :
L'aire de la surface coloriée est A(x0 + h) - A(x0)
On a h f(x0) ≤ A(x0 + h) - A(x0) ≤ h f(x0 + h), puisque f est croissante sur I.
Selon que h > 0 ou h < 0 , on a :
f(x0) ≤
h)x(A)hx(A 00 
≤ f(x0 + h) ou f(x0 + h) ≤
h)x(A)hA(x 00 
≤ f(x0)
Or, f est continue sur I, donc
0h
lim
f(x0 + h) = f(x0) , et d'après le théorème des gendarmes, il en résulte
h)x(A)hx(A
lim 00
0h
= f(x0).
Donc A est dérivable en x0 et A'(x0) = f(x0) pour tout x0 de I.
Donc A est une primitive de f sur I
Soit F une primitive quelconque de f sur I alors A(x) = F(x) + C
Or A(a) = 0, d’où : A(a) = F(a) + C = 0
C = - F(a)
Et A(x) = F(x) – F(a)
2. Primitive d’une fonction continue
Théorème admis :
Soit f une fonction continue sur un intervalle [a ; b]
La fonction Φ définie sur [a ; b] par Φ(x) =
x
adt)t(f
est :
L’unique primitive de f sur [a ; b] qui s’annule en a
Remarques
• La fonction Φ, définie dans le théorème, est donc dérivable sur [a ; b] , de dérivée f
Ce résultat montre que toute fonction continue sur [a ; b] admet une, donc des primitives sur [a ; b]
Plus généralement, toute fonction continue sur un intervalle I quelconque admet des primitives
• Soit F une primitive quelconque de f sur [a ; b], alors
b
adt)t(f
= F(b) - F(a)

3/8
3. Généralisation de l’intégrale à l’aide d’une primitive
Propriété et définition
Soit f une fonction continue sur un intervalle I et F une primitive quelconque de f sur I. Pour tous réels
a et b de I, la différence F(b) - F(a) ne dépend pas de la primitive de f choisie
On définit alors l'intégrale de a à b de f par
b
adt)t(f
= F(b) - F(a)
Exemple
La fonction polynôme f : x x2 - 1 est continue sur ℝ
L'une de ses primitives est F : x
3
x3
- x
On a ainsi :
1
1dx)1²x(
= F(1) - F(- 1) = (
3
1
- 1) - (
3
1
+ 1) =
3
2
- 2 =
3
4
§ 3 Propriétés de l’intégrale
1. Relation de Chasles
Soit f une fonction continue sur un intervalle I. Pour tous réels a, b et c de I, on a :
c
adx)x(f
=
b
adx)x(f
+
c
bdx)x(f
Démonstration :
Soit F une primitive de f sur I
b
adx)x(f
+
c
bdx)x(f
= F(b) – F(a) + F(c) – F(b) = F(c) – F(a) =
c
adx)x(f
Remarques :
Lorsque f est positive sur I et si a ≤ b ≤ c, la relation de Chasles
traduit que l'aire du domaine hachuré est la somme des aires
des deux domaines D1 et D2
En prenant c = a et du fait que
a
adx)x(f
= 0, on obtient :
a
bdx)x(f
=
b
adx)x(f
2. Linéarité
Soit f et g deux fonctions continues sur un intervalle I et k un réel.
Pour tous réels a et b de I, on a :
b
adx)x)(gf(
=
b
adx)x(f
+
b
adx)x(g
et
b
adx)x)(f.k(
= k ×
b
adx)x(f
Démonstration :
Si F et G sont des primitives de f et g sur I, alors F + G est une primitive de f + g, et kF une primitive
de kf sur I

4/8
3- Intégrales et inégalités
Soit f une fonction définie et continue sur un intervalle I de ℝ , et a, b deux réels appartenant à I.
(1) Si a ≤ b et f ≥ 0 sur l'intervalle I, alors
b
a
dx)x(f
≥ 0.
(2) Si a ≤ b et f ≤ 0 sur l'intervalle I, alors
b
a
dx)x(f
≤ 0.
(3) Si a ≥ b et f ≥ 0 sur l'intervalle I, alors
b
a
dx)x(f
≤ 0.
(4) Si a ≥ b et f ≤ 0 sur l'intervalle I, alors
b
a
dx)x(f
≥ 0.
Exemple :
Déterminer le signe de l’intégrale
2
1
1
dxxln
4- Conservation de l’ordre
Soit f et g deux fonctions continues sur [a ; b]. Si f ≤ g sur [a ; b], c'est-à-dire si, pour tout réel x de
[a ; b], f(x) ≤ g(x) , alors
b
a
dx)x(f
≤
b
a
dx)x(g
Démonstration :
Si f ≤ g sur [a ; b] , alors, pour tout réel x de [a ; b] , g(x) - f(x) ≥ 0 .
D'autre part, g - f est continue sur [a ; b] .
D'après la propriété de positivité, on obtient
b
a
dx)]x(f)x(g[
≥0
puis, par linéarité,
b
a
dx)x(g
-
b
a
dx)x(f
≥ 0 ; d'où le résultat.
Lorsque f et g sont positives sur [a ; b], l'inégalité traduit le fait que l'aire du
domaine D1 situé sous Cf, est inférieure à l'aire du domaine D2 situé sous Cg

5/8
5- Inégalités de la moyenne
Soit f une fonction continue sur un intervalle I, et a et b deux réels de I.
 Si a ≤ b et s'il existe deux réels m et M tels que m ≤ f (x) ≤ M, pour tout réel x de [a ; b]
alors m(b – a) ≤
b
a
dx)x(f
≤ M(b – a)
 S'il existe un réel M positif tel que | f | ≤ M sur I, alors
b
a
dx)x(f
≤ M | b – a |
Démonstration :
Pour tout réel x de [a ; b] , on a : m ≤ f (x) ≤ M, donc, par conservation de l'ordre, on obtient :
b
a
dxm
≤
b
a
dx)x(f
≤
b
a
dxM
ce qui donne le résultat puisque
b
a
dx
= b - a .
Remarques :
Lorsque a ≤ b et f positive, ainsi que m, cet encadrement traduit que
l'aire du domaine D est comprise entre les aires des deux rectangles
de hauteurs m et M et de largeur b - a . L'encadrement montre aussi que la valeur moyenne μ de f sur
[a ; b] est comprise entre m et M.
Exemple :
Pour tout réel x de [1 ; 8] ,on a
2
≤
x1
≤ 3, donc :
7
2
≤
8
1
dxx1
≤ 21