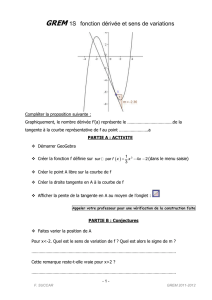
Approche intuitive 1. Préambule Quelques remarques et définitions

Approche intuitive
1. Préambule
Quelques remarques et définitions s’imposent avant de proposer une reconstruction
de l’approche intuitive que permet d’avoir une figure donnée, à propos du théorème
de Rolle et de sa généralisation.
1. Afin de simplifier cet exposé, nous considérerons que les fonctions étudiées sont
toutes réelles, les intervalles seront des intervalles de R.
2. Je suppose connues les notions de limites d’une fonction, je rappelle cependant
qu’une fonction réelle est continue sur un intervalle si et seulement si :
)()(lim afxf
ax 
, pour tout point a de l’intervalle
Dire qu’un fonction est continue en a implique donc en particulier que l’on peut
toujours [trouver un x tel que] rendre la différence entre f(x) et f(a) soit aussi petite
que l’on veut, pour peu que l’on choisisse x suffisamment proche de a.
1
3. Pour comprendre ce qui va suivre il faut connaître la notion de dérivée et son
interprétation géométrique. Je rappelle donc rapidement les conditions de dérivabilité
d’une fonction réelle :
définition 1 :
Une fonction f définie sur un intervalle non trivial est dite dérivable en
un point a, a I, si et seulement si :
1
La définition moderne et formelle de la continuité est la suivante : f définie sur I est continue en a si et
seulement si pour tout  > 0, il existe  > 0 tel que pour x I| x-a |≤  | f(x)-f(a) |≤ 
l
ax afxf
ax 
)()(
lim

Si c’est le cas, cette limite s’appelle la dérivée de f en a et elle est notée
f’ (a)
définition 2
Une fonction f est dérivable sur I si elle l’est en tout point de I. La
dérivée de f est alors la fonction définie sur I qui associe à tout point x
de I le nombre f’(x).
4. Interprétation géométrique
La dérivée d’une fonction permet en fait de calculer le coefficient directeur de la
tangente à la courbe représentative de la fonction partout où celle-ci est dérivable.
En effet, considérons la représentation suivante :
Le rapport
ax afxf
)()(
(que l’on appelle coefficient directeur de la droite qui passe
par A (a, f(a)) et B (x,f(x))) s’interprète comme la pente, ou l’inclinaison, de la droite
(AB). Si la fonction est continue, f(x) tend vers f(a) lorsque x tend vers a et donc le
point B tend vers A. Lorsque la fonction est dérivable, la limite lorsque x tend vers a
du rapport ci-dessus existe et la droite (AB) admet donc un position limite : c’est la
tangente à la courbe au point A (en rouge sur la figure). Ainsi, la condition de

dérivabilité en un point a, exprimée de façon géométrique, traduit l’existence d’une
tangente au point A (a,f(a)) à la courbe représentative de la fonction f.
Enfin, on remarquera que lorsque la tangente en un point est ”croissante“, la valeur
de la dérivée en ce point est positive et elle est négative si la tangente est
“décroissante“.
Remarque : La notion de tangente est une notion mathématique très compliquée et
qui peut être abordée et caractérisée de multiples façons différentes
2
. Le point de
vue que j’ai sélectionné ici est dynamique dans le sens où l’on y considère la
tangente en un point A comme la position limite d’une corde (AB). Il y a donc derrière
ce point de vue une idée de mouvement : le point B parcours la courbe jusqu’à ce
qu’il atteigne le point A. On peut alors remarquer que l’on peut considérer la tangente
comme la position limite de la corde (AB) indifféremment de la position initiale du
point B, que ce dernier soit situé à gauche ou à droite du point A.
.
1. Première approche du théorème
Considérons à présent une figure représentant une fonction continue sur un
intervalle et ayant la même valeur aux bornes de cet intervalle :
2
Il est bien entendu possible de relier entre eux les divers points de vue sur la tangente. Le lien qui est unit est
basé fondé sur le théorème de Rolle lui-même.

Je propose de décrire un raisonnement intuitif et empirique (c’est-à-dire que c’est
l’expérimentation qui guide l’intuition) qui va nous conduire vers le théorème de
Rolle. Pour ce faire, je me dégage pour l’instant de toute rigueur mathématique, au
sens fort du terme, pour ne conserver que des résultats et des hypothèses guidées
par des expériences successives sur la figure. Dans un premier temps, j’omets donc
volontairement de souligner les erreurs mathématiques souterraines que contient le
raisonnement proposé.
A partir de cette configuration, on peut évaluer de manière empirique l’allure
générale des tangentes à la courbe. Un bref examen permet de constater que ces
dernières sont décroissantes du point A au point C, puis croissante du point C au
Attention A, B et C ne sont pas sur la figure… et vous parlez de la seconde figure !
point B. En particulier, sur cette figure, la tangente à la courbe au point C est
horizontale (en rouge). Peut-on pour autant en conclure que toute courbe qui relie de
a
c
c
c
b
f(a)=f(b)
Figure A

façon continue deux points de même hauteur admet toujours ‘quelque part’ une
tangente horizontale ? Afin d’éviter les contingences liées à une configuration en
particulier, on peut imaginer différentes configurations possibles :
Soit le point A et le point B sont reliés par une courbe horizontale (figure 1), c’est-à-
dire par une droite, auquel cas la tangente à la courbe est confondue avec la courbe
elle-même et donc il y a bien une tangente horizontale (en fait la tangente en chaque
point est horizontale)
Soit le point A et le point B sont reliés par une courbe non horizontale (figure 2). En
fait, la figure 2 peut se ramener sans perte de généralité à la figure A initialement
proposée
3
.
Il y a donc en fait deux types de configurations possibles : la première (courbe
horizontale) ne pose pas de difficulté, la seconde peut se ramener en fait à la
configuration de la figure A. Raisonnons donc à partir de cette dernière.
3
Il suffit en fait de découper tout d’abord l’intervalle de définition afin de se ramener à une figure du type de la
figure A, puis de répéter le même raisonnement à chaque partie de l’intervalle [dans la mesure, évidemment où
la figure donne une idée suffisamment correcte des changements du sens de variation…]
a
b
a
b
Fig.1 Fig.2