TS - DEVOIR N°1 A RENDRE LE SEPTEMBRE 2009

TS - DEVOIR N°1 A RENDRE LE 9 SEPTEMBRE 2009
Partie A
Soit (a, b, c) 3, la fonction f : x x3 + ax2 + bx + c et C la courbe représentative de f
dans un repère orthonormé
j , i ; O
.
Déterminer les réels a, b, c sachant que :
 f admet un extremum en 2 et un extremum en – 2 ;
 la tangente  au point de C d’abscisse nulle passe par A(1 ; - 9).
Partie B
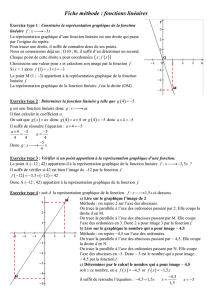
Soit f la fonction définie sur  par : f(x) = x3 – 12x + 3.
On désigne par C sa courbe représentative dans un plan P rapporté au repère orthogonal
j , i ; O
(unité : 2 cm sur l’axe des abscisses, ½ cm sur l’axe des ordonnées).
1. a. Déterminer le sens de variation de la fonction f.
b. Déterminer les limites aux bornes de son ensemble de définition.
c. Dresser le tableau de variation de la fonction f.
2. Calculer les coordonnées du point d’intersection de C avec l’axe des ordonnées du
repère. Donner à 10- 1 près, à l’aide de la calculatrice, les coordonnées des points
d’intersection de C avec l’axe des abscisses.
3. Soit h , M et M’ deux points de C d’abscisses respectives h et (- h).
Montrer que le milieu I du segment [MM’] est indépendant du réel h.
Que peut-on en déduire pour la courbe C ?
4. a. Déterminer une équation de la tangente T à C au point I.
b. Etudier la position de C par rapport à T.
5. Tracer la courbe C et la tangente T dans le repère
j , i ; O
.

TS – Corrigé du devoir sur feuille n° 1 du 9 septembre 2009
Partie A
f est une fonction polynôme donc f est définie et dérivable sur . De plus f ’(x) = 3x2 + 2ax + b.
f admet un extremum en 2 et un extremum en (- 2) si, et seulement si, f ’(x) s’annule et change de signe en
2 et (- 2). Or, f ’(x) est un polynôme du second degré en x. On en déduit que f ’(x) change de signe à
chacune de ses racines dès que f ’(x) admet deux racines distinctes.
Donc f admet un extremum en 2 et un extremum en (- 2) si, et seulement si, f ’(2) = 0 et f ’(- 2) = 0.
D’autre part, la tangente  au point de C d’abscisse nulle a pour équation réduite :
y = f ’(0)(x – 0) + f(0) où f ’(0) = b et f(0) = c.
Par conséquent  a pour équation réduite : y = bx + c.
Enfin,  passe par le point A(1 ; - 9) si, et seulement si, les coordonnées de A vérifient l’équation réduite
de  soit : - 9 = b + c.
En résumé, les réels a, b et c, s’ils existent, sont solutions du système :
3 c
0 a
12 - b
c b 9 -
0 b 4a - 12
0 b 4a 12
Par conséquent il existe une fonction f et une seule solution du problème posé. Elle est définie sur  par :
Partie B
1. a. La fonction f à étudier est celle déterminée dans la Partie A. Donc on peut immédiatement écrire :
f ’(x) = 3x2 – 12  f ’(x) = 3(x – 2)(x + 2).
Ainsi : f ’(x) > 0  x  ]- ∞ ; - 2[  ]2 ; + ∞[
f ’(x) = 0  x = - 2 ou x = 2
f ’(x) < 0  x  ]- 2 ; 2[.
On en déduit que f est strictement croissante sur chacun des intervalles ]- ∞ ; - 2] et [2 ; + ∞[ et strictement
décroissante sur l’intervalle [- 2 ; 2].
b.
  - f lim donc xlim f lim
3
x
.
De même
 f lim
.
Soit f une fonction numérique, D désigne son ensemble de définition et C sa courbe
représentative dans un repère
j , i ; O
.
Axe de symétrie
La droite d ‘équation x = a est axe de symétrie de la courbe C si, et seulement si :
D est symétrique par rapport à a et f(a + h) = f(a – h),
le réel h étant un réel quelconque tel que (a + h) et (a – h) appartiennent à D .
Centre de symétrie
Le point (a ; b) est centre de symétrie de la courbe C si, et seulement si :
D est symétrique par rapport à a et f(a + h) + f(a – h) = 2b.
f(x) = x3 – 12x + 3.

c. On résume ces résultats dans le tableau de variation de f
2. La courbe C coupe l’axe des ordonnées si, et seulement si, il existe un couple (x ; y) solution du
système formé par les équations respectives de la courbe C et de l’axe des abscisses :
0 x
3 y
0 x
3 12x - xy 3
.
Donc la courbe C coupe l’axe des ordonnées au point de coordonnées :
A l’aide de la touche « trace » de la calculatrice on détermine les coordonnées des points d’intersection de
la courbe C avec l’axe des abscisses soit :
3. M et M’ désignent deux points de la courbe C d’abscisses respectives h et (- h), h décrivant . Leurs
ordonnées respectives sont donc :
f(h) = h3 – 12h + 3 et f(- h) = - h3 + 12h + 3.
Alors, le milieu I du segment [MM’] a pour coordonnées :
xI =
2h) (- h 
 xI = 0 et yI =
2h) f(- f(h) 
 yI = 3.
Par conséquent, lorsque h décrit , les points M et M’ se déplacent le long de la courbe C en restant
symétriques l’un de l’autre par rapport au point fixe I(0 ; 3).
On a ainsi démontré que :
4. a. La tangente T en I à la courbe C est la droite  de la Partie A. Donc T a pour équation :
b. Pour connaître la position de la courbe C par rapport à sa tangente T on considère deux points N et P,
de même abscisse x, placés respectivement sur la courbe C et sur la droite T.
La position de C par rapport à T sera donnée par le signe de la différence des ordonnées, yN - yP, de ces
deux points. yN - yP = x3.
Donc yN - yP > 0  x > 0,
yN - yP = 0  x = 0,
yN - yP < 0  x < 0.
En conclusion,
x
- ∞
+ ∞
f ’(x)
+
-
+
f
- 2
2
0
0
- ∞
+ ∞
19
- 13
(0 ; 3)
(- 3,5 ; 0), (0,2 ; 0) et (3,3 ; 0).
la courbe C admet le point I(0 ; 3) pour centre de symétrie.
y = - 12x + 3.
la courbe C est au-dessous de T pour tous les points d’abscisses négatives
et au-dessus de T pour tous les points d’abscisses positives.