Fiche Démonstration

Fiche Démonstration Triangle Rectangle 4e
Démonstration de la propriété :
Si un triangle est rectangle, alors il est inscrit dans un cercle
dont le diamètre est son hypoténuse.
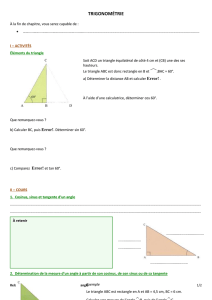
 Soit un triangle ABC rectangle en B, et O le milieu de [AC].
 Soit D le symétrique de B par rapport à O, alors O est le milieu
du segment [BD].
 Les diagonales du quadrilatère ABCD se coupent en leur milieu,
donc ABCD est un parallélogramme.
 Puisque le parallélogramme ABCD possède un angle droit, alors
c’est un rectangle.
 Or, dans un rectangle, les diagonales sont de même longueur, donc
OA=OB=OC.
 Ce qui signifie que le triangle ABC est inscrit dans le cercle de
centre O, c’est-à-dire de diamètre [AC].
Démonstration de la propriété :
Si un triangle est inscrit dans un cercle dont le diamètre est l’un
de ses côtés, alors il est rectangle.
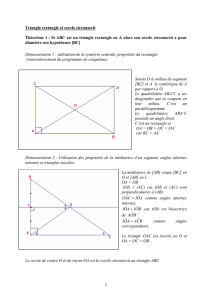
 Soit un cercle de centre O et de diamètre [BC], et un point A de
ce cercle tel que Æ;OAB=x° et Æ;OAC=y°.
 Les segments [OB], [OC] et [OA] sont des rayons du cercle de
centre O, donc les triangles BAO et CAO sont isocèles en O.
 Les angles adjacents à la base d’un triangle isocèle étant de
même mesure, on déduit que Æ;ABO=x° et Æ;ACO=y°.
 D’autre part, la mesure de l’angle Æ;BAC vaut x+y°.
Dans le triangle ABC, on a, d’après la somme des angles d’un
triangle,
Æ;ABC + Æ;CAB + Æ;BCA = 180°.
Il vient donc que 2x+2y=180°

En factorisant, on déduit que 2(x+y)=180° ;
Donc finalement Æ;BAC = x+y = 90° ;
 Cela signifie que le triangle ABC est rectangle en A.