Pour tous les exercices, on impose la contrainte suivante : après

Pour tous les exercices, on impose la contrainte suivante : après avoir déplacé les
différents éléments de la figure, celle-ci doit encore respecter les consignes de
l'énoncé ; ceci, pour montrer aux élèves la différence entre dessiner et construire.
Parallèles et perpendiculaires
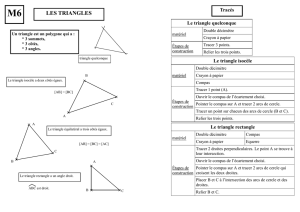
Quelques constructions (6ème et 5ème) visant à mieux assimiler le vocabulaire de base :
 Tracer trois points A,B et C non alignés. Tracer la droite (AB),le segment [AC];Tracer la droite perpendiculaire à (AB)
passant par B et tracer la droite parallèle à (AB) passant par C.Ces deux droites se coupent en un point D.
 Tracer deux droites sécantes d1 et d2. Placer un point A qui n'appartienne ni à d1, ni à d2. Tracer la droite parallèle à d1
passant par A et la droite parallèle à d2 passant par A.
 Tracer un triangle ABC. Tracer la droite perpendiculaire à (BC) passant par A et la droite perpendiculaire à (AC) passant par
B.
 Tracer un triangle ABC,puis le point M, milieu de [AB]. Tracer la droite parallèle à (BC) passant par M;elle coupe (AC) en
N. Tracer la droite parallèle à (AC) passant par M;elle coupe (BC) en P. Tracer (AP) et (BN); Ces deux droites se coupent en
I.
Tracer un triangle ABC,puis un point M sur le segment [AB].
Tracer la droite parallèle à (BC) passant par M;elle coupe (AC) en N.
Tracer la droite parallèle à (BA) passant par N;elle coupe (BC) en P.
Tracer la droite parallèle à (AC) passant par P;elle coupe (AB) en R.
Tracer la droite parallèle à (BC) passant par R;elle coupe (AC) en S.
Tracer la droite parallèle à (BA) passant par S;elle coupe (BC) en T.
Tracer la droite parallèle à (AC) passant par T;elle coupe (AB) en U.
Que constate-t-on ?
Quelques figures à reproduire (6ème et 5ème) visant à aider l'élève à rédiger un programme de construction:
A
B
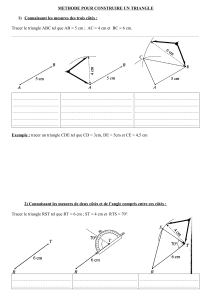
Tracer ces figures en commençant par le triangle ABC:

B
A
C
(d)
d est parallèle à (BC)
B
A
C
C
A
B
M
PN

C
A
B
(AC) parallèle à (BK)
K
C
BA
H(HD) parallèle à (CB)
D
QUELQUES EXERCICES DONNES EN CINQUIEME DANS LE CADRE DE PARCOURS
DIVERSIFIES :
Construire un segment [AB] et le cercle de diamètre [AB].
Construire un triangle ABC rectangle en A et marquer l'angle de sommet A.
Construire un triangle équilatéral et mesurer les 3 côtés
Déplacer les sommets et vérifier que le triangle reste équilatéral.
Construire un triangle ABC isocèle en A (mais pas équilatéral);mesurer les trois côtés, déplacer les points A,B,C et vérifier que le
triangle reste isocèle.
Construire un segment avec le BOUTON 3 (segment)
Le nommer [AB] avec le BOUTON 9 (nommer).
Construire la médiatrice de [AB].
Placer un point sur la médiatrice avec le BOUTON 2 (point sur un objet ).
Nommer ce point M ,puis mesurer les segments [MA] et [MB] à l'aide du BOUTON 8 (distance et longueur).
Déplacer le point M et observer.
Que constate-t-on?
Pouvait-on prévoir ce résultat? Pourquoi?
Construire une droite et la mettre en rouge avec le BOUTON 10 (couleur).
Créer un point et le nommer M.Trouver une méthode pour construire le symétrique du point M par rapport à la droite rouge(sans
utiliser le BOUTON 6);le nommer M'.
Déplacer le point M et vérifier que le point M' reste toujours le symétrique de M .
Rendre invisible les traits de construction avec le BOUTON 10 ( cacher/montrer).

Créer deux autres points N et P ; construire leur symétrique N' et P' par rapport à la droite rouge;rendre invisible tous les traits de
construction.
Construire le triangle MNP;le mettre en vert.
Construire le triangle M'N'P'.
Déplacer les points M, N et P;observer.
Construction d'un pentagone régulier
 Tracer un segment [AK], un cercle de diamètre [AK] et de centre O,puis une droite perpendiculaire à [AK] qui coupe le
cercle en B.
 Placer le point Q ,milieu de [OB] et le point P sur le segment [OK] tel que OP est égale au quart du rayon du cercle.
 Tracer le cercle de centre P ,de rayon [PQ];ce cercle coupe le diamètre [AK] en deux points qu'on appelle I et J.
 Tracer la perpendiculaire à [AK] passant par J;elle coupe le grand cercle en deux points appelés C et D.
 Tracer la perpendiculaire à [AK] passant par I;elle coupe le grand cercle en deux points appelés E et F.
Les cinq points A,D,F,E,C forment un pentagone régulier; si on numérote 1,2,3,4,5 ces cinq points dans l'ordre dans lesquels ils se
trouvent sur le cercle et si on relie les points de la façon suivante:
135241, on obtient une étoile à 5 branches.
 Construire un triangle ABC à l'aide du BOUTON 3 (TRIANGLE).
 Construire la hauteur issue de A;la mettre en rouge à l'aide du BOUTON 9(COULEUR)
 Construire la hauteur issue de B; la mettre en vert.
 Déplacer les points A,B,C pour que la hauteur issue de A soit à l'extérieur du triangle et la hauteur issue de B soit à l'intérieur du
triangle.
 Construire un triangle ABC .
 Construire la médiatrice de [BC] à l'aide du BOUTON 5 (MEDIATRICE);la nommer d.
 Déplacer les sommets du triangle, observer, puis placer le point A sur la droite d.
Quelle est alors la nature du triangle ABC ? Pourquoi?
 Déplacer le point A pour qu'il ne soit plus sur la droite d;construire la hauteur issue de A;la nommer d'.
Comment semblent être les droites d et d'?
Est-ce toujours vrai(ne pas hésiter à déplacer les points)? Pourquoi?
 Déplacer les points pour que les droites d et d' ne forment plus qu'une droite;quelle est la nature du triangle ABC ? Pourquoi ?
 Construire un triangle ABC.
 Marquer les angles ABC et ACB à l'aide du BOUTON 8 (MARQUER UN ANGLE), puis les mesurer à l'aide du BOUTON 7(
MESURE D'ANGLE)
Sans construction supplémentaire déplacer les points pour que ABC soit isocèle en A.
a) Construire un triangle ABC,puis la médiatrice de [AB] et de [BC]à l'aide du BOUTON 5 (MEDIATRICE).
b) Appeler I le point d'intersection des 2 médiatrices.
Tracer les segments [IA],[IB],[IC] et les mettre en rouge.
c) Mesurer les longueurs IA,IB,IC.Que constate -t-on? Est-ce toujours vrai?Pouvait-on prévoir ce résultat?Pourquoi?
a) Construire un triangle ABC et son cercle circonscrit.
Déplacer les points A,B et C;si le cercle ne passe plus par les points A,B et C refaire la construction.
b) Marquer les angles ABC,ACB et CAB à l'aide du BOUTON 8, puis les mesurer. Déplacer les points A,B et C et observer les
mesures des angles.
A quelle condition sur les angles du triangle le centre du cercle circonscrit est à l'intérieur du triangle? Puis à l'extérieur du triangle?
Puis sur un côté du triangle?
a) Construire un quadrilatère quelconque ABCD,puis les médiatrices de [AB],de [BC] et de [CD];mettre les médiatrices en rouge.
b) Déplacer les points pour que les 3 médiatrices soient concourantes;tracer alors le cercle circonscrit au quadrilatère ABCD.
c) Sans la tracer, répondre à la question:que va faire la médiatrice de [AD] ? ... puis tracer et vérifier
 Construire deux segments [AB] et [BC].

 A l'aide de droites parallèles construire le point D tel que ABCD soit un
parallélogramme.
 Donner la propriété qui justifie cette construction.
 Construire un segment [AC] et un point B.
 En utilisant une autre méthode qu'à l'exercice 1, placer le point D tel que ABCD
soit un parallélogramme .
 Donner la propriété qui justifie cette construction.
 Construire deux segments [AB] et [BC].
 Construire les points D et E tels que ABCD et ACED soit des parallélogrammes.
 Rendre invisibles les traits de construction à l'aide du BOUTON 9 ( CACHER/MONTRER )
Mesurer [BC] et [CE] ; que constate-t-on ? Déplacer les points A,B,C ; est-ce toujours vrai ? Justifier.
 Construire un triangle SRT et placer un point U sur le segment [SR] à l'aide du
BOUTON 2 ( POINT SUR UN OBJET )
 La parallèle à (RT) passant par U coupe (ST) en V
 La parallèle à (ST) passant par U coupe (RT) en H
 La parallèle à (RS) passant par V coupe (RT) en KNommer deux quadrilatères dont on est sûr qu'ils sont des
parallélogrammes ; justifier
 Mesurer [TH] et [KR] ; que constate-t-on ?
Déplacer le point U ; est-ce toujours vrai ? Expliquer.
Construire un segment [AB] et placer un point C. Imaginer une méthode pour tracer un cercle de centre C et de rayon la longueur du
segment [AB], puis effacer les traits de construction. Déplacer le point B ; si la construction est juste, le rayon du cercle est toujours
de même mesure que le segment [AB].
Reproduire la figure suivante sachant que ABCD et ABFE sont des parallélogrammes;on
rendra invisible les traits de construction :
A B
FE
DC
 Construire un rectangle ABCD .
 Tracer et mesurer les segments [ ] AC et [ ] BD puis déplacer les points A,B,C,et D.
Que constate-t-on ? Pourquoi?
 Construire un segment [AC], puis construire les point B et D pour que ABCD soit un losange.
 Mesurer l'angle BAC et déplacer les points de manière à obtenir BAC = 25 °(si ce n'est pas possible, il faut refaire la figure).
 Construire un segment [AB], puis construire les point C et D pour que ABCD soit un losange en utilisant uniquement les 4
premiers boutons de la barre de menu.
 Mesurer l'angle BAD et déplacer les points de manière à obtenir BAD = 30 °(si ce n'est pas possible, il faut refaire la figure).