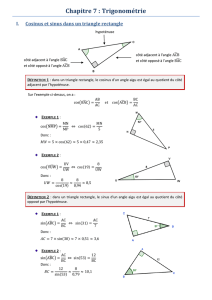
fonctions usuelles

1
14 / les fonctions de référence
pour toute fonction, le schéma d’étude est le même :
ensemble de définition, tableau de variations, graphique.
les fonctions affines
Ce sont les fonctions de type
f x ax b( )  
. Elles sont définies sur
R
.
tableau de variations dans le cas général :
pour a > 0
x
ax b
pour a < 0
x
ax b
graphique : une droite, montante si a > 0, descendante si a < 0
Avec la figure ci-contre,
l x( )
désigne la longueur OB,
p x( )
le
périmètre de ABCD et
a x( )
l’aire de ABCD. Montrez que l, p et a
sont des fonctions affines.

2
les fonctions affines engendrent
les fonctions affines par intervalle
Donner l’expression algébrique de la fonction dans chacun des cas suivants :

3
la fonction carré
C’est la fonction
x x2
. Elle est définie sur
R
.
tableau de variations :
x
0
x2
0
graphique : une parabole tournée vers le haut, passant par
l’origine et par les points
( ; )11
et
)1;1(
.
Cette parabole possède une symétrie remarquable, par rapport à l’axe des ordonnées. Ceci est
caractéristique des fonctions paires.
une fonction est paire quand deux réels quelconques opposés ont la même image :
pour tout réel x pour lequel f est définie, f(–x) = f(x).
Le graphique de la fonction est alors symétrique par rapport à l’axe des ordonnées.
Toutes les fonctions de type
xax2
sont des fonctions paires, ayant pour graphique des
paraboles passant par l’origine.
tableau de variations dans le cas général :
pour a > 0
x
0
ax2
0
pour a < 0
x
0
ax2
0

4
retrouvez l’équation de chaque parabole comme une fonctions de type
xax2
:
C1
C2
C3
C4
C5
C6
C1
C2
C3
C4
C5
C6
montrez que dans ces trois cas, les fonctions sont du type
xax2
:
f(x) est l’aire d’un triangle
rectangle isocèle de côté x
f(x) est l’aire d’un triangle
équilatéral de côté x.
x est le rayon du cercle inscrit
dans un carré de côté a, f(x) est
l’aire du domaine compris entre
le cercle et le carré..
exercice 63 page 131
exercice 67 page 131

5
la fonction inverse
C’est la fonction
xx 1
. Elle est définie sur
R
*.
tableau de variations :
x
0
1
x
||
graphique : une hyperbole passant par les points
( ; )11
et
( ; ) 1 1
,
dont les axes sont les asymptotes.
Cette hyperbole possède une symétrie remarquable par rapport à l’origine. Ceci est
caractéristique des fonctions impaires.
Une fonction est impaire quand deux réels quelconques opposés ont des images opposées :
pour tout réel x pour lequel f est définie, f(–x) = –f(x).
Le graphique de la fonction est alors symétrique par rapport à l’origine du repère.
Toutes les fonctions de type
xa
x
sont des fonctions impaires, et les axes du repères sont
les asymptotes de leurs graphiques.