Sur la figure ci-contre, le doigt exerce sur la punaise une force de 15 N

Mécanique des fluides – TSI CF 2013 - Exercices basiques
Exercice N° 1 – Calculs des pressions Hydrostatique
Deux points situés dans l'eau sont à 10 m l'un au-dessus de l'autre.
La masse volumique de l'eau étant ρ = 1000 kg·m-3
Calculer la différence de pression entre ces deux points.
Exercice N° 2 – Hydrostatique - Calculs des pressions dans un cric
L’utilisateur d’un cric exerce une force F de 150 N sur le piston A.
Les pistons ayant des sections circulaires de diamètres respectifs
D1 = 45 mm pour le piston A et D2 = 90 mm pour le piston B.
Calculer la force F’ exercée par le fluide sur le piston B. Pourra-t-il lever
une charge de 600N ?
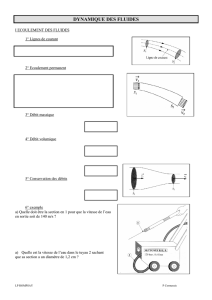
Exercice N° 3 – Hydrodynamique - Calculs de débit dans un écoulement
Dans un tube de diamètre intérieur d = 12,7 mm s'écoule, à la vitesse moyenne
de 1,2 m/s, de l'huile d’olive de masse volumique 820 kg/m³.
Calculer le débit volumique Qv et le débit massique Qm
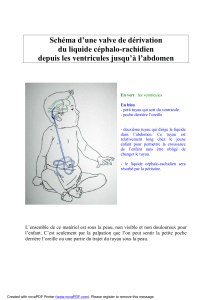
Exercice N° 4 – Hydrodynamique – Nettoyeur haute pression
On étudie un nettoyeur haute pression de 120 bars et débit de 8.4 l/min
1. Quelle doit être la section en (1) pour que la vitesse de l'eau en sortie soit de 140 m/s ?
2. Quelle est la vitesse de l'eau dans le tuyau (2), sachant que sa section a un diamètre
de 1,2 cm ?
Exercice N° 5 – Hydrodynamique – Pompage et régime d’écoulement
Une pompe permet le transport d'un liquide, de masse volumique 840 kg/m3, dans un tuyau de diamètre
intérieur 50 mm.
Le débit de la pompe est de 12,5 m3/h.
La pompe, à piston rotatif, a une fréquence de rotation de 920 tr/min.
1) Calculer la vitesse du liquide à la sortie de la pompe.
2) Calculer la cylindrée de la pompe.
La viscosité dynamique du liquide est 0,50 Pa.s. La vitesse du liquide est 1,77 m/s.
3) Calculer la viscosité cinématique.
4) Calculer le nombre de Reynolds.
5) En déduire le régime d'écoulement du liquide dans le tuyau.
Formulaire
Q : débit en m3/s n ou f : fréquence de rotation en tr/s Cyl : cylindrée en m3/tr
D : diamètre intérieur du tuyau en m S : section intérieure du tuyau en m2
V : vitesse du liquide en m/s ρ : masse volumique du liquide en kg/m3
μ : viscosité dynamique en Pa.s ν : viscosité cinématique en m2/s Re : nombre de
Reynolds
Cyl = Q . n Q = S × v ν = μ / ρ Re = V × D / 
10 m
B
A
10 m
B
A