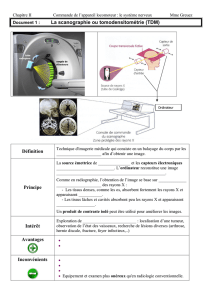
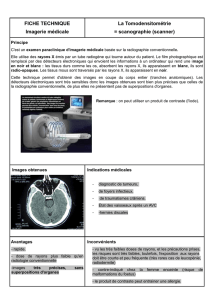
Principes de l`optique géométrique

Optique Géométrique et Ondulatoire
Optique géométrique
Indice d’un Milieu et Chemin optique
Définition
On appelle indice n d’un milieu le rapport de la célérité c de la lumière dans le vide à la célérité v
(vitesse de phase) de la lumière dans un milieu :
N = c / v
Si n est constant en tout point du milieu, il est homogène.
Si n dépend de la longueur d’onde (donc la couleur) de la lumière, le milieu est dispersif.
Chemin optique
Le chemin optique LA1A2 entre 2points A1 et A2 est la longueur parcourue par la lumière dans le
vide pendant le même temps t2 – t1 qu’elle mettrait à parcourir le trajet A1A2 dans le milieu
considéré d’indice n :
LA1A2 = intt1t2(c.dt)= intA1A2(n.ds)
Car c.dt = n.v.dt = n.ds
D’après (1) où ds est l’élément de longueur curviligne du trajet A1A2.
Principes de l’optique géométrique : Lois de Snell Descartes
Les 3 principes de l’optique géométrique
La marche des rayons lumineux obéit à 3 principes :
 Principe de propagation rectiligne : Dans un milieu homogène, la lumière se propage en
ligne droite entre 2 points A1 et A2 de ce milieu.
 Principe du retour inverse : Entre 2 points A1 et A2 de milieux quelconques, le trajet du
rayon lumineux est indépendant du sens de parcours de la lumière.
 Principe de Fermat : Le trajet effectivement suivi par la lumière entre 2 points A1 et A2 est
celui pour lequel le chemin optique LA1A2 = [A1A2] est extrémal (en général minimal), soit :
dLA1A2 = 0
Remarques : Ces principes ne seront plus valables si :
 Les rayons lumineux ne sont pas indépendants entre eux (phénomènes d’interférences)
 La lumière traverse de brusques variations d’indice ou de transparence localisées dans une
zone étroite (phénomène de diffraction).

Variations du chemin optique
Lorsque la lumière suit le trajet A1IA2 où I est le point d’incidence sur le dioptre qui sépare 2 milieux
homogènes d’indices n1 et n2, le chemin optique entre A1 et A2 est :
LA1A2 = [A1IA2] = n1A1I + n2 . I . A2
LA1A2 = [A1IA2] = n1.u1.A1I + n2.u2.I.A2
Où u1 et u2 sont les vecteurs unitaires des segments A1I et IA2 orientés positivement dans le sens de
propagation de la lumière.
Lorsque le point d’incidence I du dioptre (n1-n2) subit un petit déplacement II’ = dI, le chemin
optique LA1A2 = [A1IA2] subit la variation :
DLA1A2 = (n1.u1 – n2u2)dI
dLA1A2 représente la différence des chemins optiques entre les trajets voisins A1I’A2 et A1IA2.
Le principe de Fermat qui affirme que dLA1A2 = 0 ou [A1I’A2] = [A1IA2] permet d’établir les lois de
Snell Descartes.
Lorsqu’un milieu est hétérogène, on établit 2 relations locales : Grad L = n.u et grad n = d(nu)/ds.
Lois de Snell Descartes
Le comportement d’un rayon lumineux incident SI lors de la réflexion et de la réfraction en I, à la
surface Σ d’un dioptre (ou d’un miroir) est régi par les 2 lois de Snell-Descartes :
Loi de la réflexion : i’1 = -i1
Loi de la réfraction : n1sin i1 = n2sin i2
Tout ce passe dans le même plan.
Objet et Image. Stigmatisme et aplanétisme :
Condition de stigmatisme (Objet A et image A’)
Un système optique est dit stigmatique pour le couple (A,A’) si tous les rayons issus d’un point objet
A (source) sortent du système optique, en passant par un même point image A’.
Ainsi, le point objet A est l’intersection des rayons incidents et le point image A’ est l’intersection des
rayons émergents, à la sortie du système optique. Le point image A’ est réel si les rayons émergents
se rencontrent effectivement en A’, et A’ est virtuel si les prolongements des supports des rayons
émergents passent en A’.
La condition de stigmatisme pour les points conjugués A et A’ s’écrit donc :
LAA’ = Cte
Si 2 système optiques 1 et 2 en cascade, l’image à travers le système 1 joue le rôle d’un objet pour le
système 2.

Définition et condition d’aplanétisme
Un système optique stigmatique pour le couple de points (A,A’) est dit aplanétique si le stigmatisme
est conservé dans un plan de front.
La condition d’aplanétisme (ou condition d’Abbe) s’écrit, si A’B’ est l’image de AB :
n.AB.sin α = n’.A’B’.sin α ‘
Conditions de Gauss : Lorsque les rayons sont très peu inclinés sur l’axe du système optique, et si AB
est petit, les rayons issus de A passent au voisinage. De A’ : il y a stigmatisme approché pour les
rayons paraxiaux.