Travail de la force électrostatique
publicité

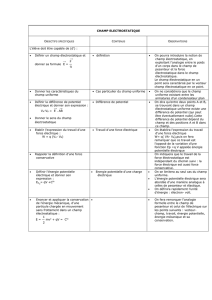
Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Activités/ questions professeur Activités/ réponses apprenants(es) Page 1 sur 6 TRACE ECRITE Chapitre 6 ENERGIE POTENTIELLE ELECTROSTATIQUE Le champ électrostatique est considéré uniforme. 1. Travail de la force électrostatique Considérons le champ Error! uniforme créé entre les armatures d’un condensateur plan. Supposons une particule de charge q en mouvement dans ce champ se déplaçant d’un point A à un point B. + A - E - + + F = q.E - B Le travail de la force électrostatique est par définition : WAB ( Error!) = Error!. Error!; or Error!= q. Error! D’où WAB ( Error!) = q Error!. Error! Remarque : Le travail de la force électrostatique est indépendant du chemin suivi. La force électrostatique est une force conservative Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 1 sur 6 OBS Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Page 2 sur 6 2. Notion de différence de potentiel (ddp) 2.1. Définition La différence de potentiel entre deux points A et B situés dans une région de l’espace où règne un champ électrostatique uniforme est égale au produit scalaire du vecteur champ 𝐸⃗ par le vecteur ⃗⃗⃗⃗⃗ 𝐴𝐵 : ⃗⃗⃗⃗⃗ VA – VB = 𝐸⃗ ∙𝐴𝐵 P B E A d N Remarque : - Elle s’exprime en volt (V) - La ddp est identique à la tension UAB = VA – VB - Le potentiel caractérise l’état électrique en un point. 2.2. Propriétés du potentiel électrostatique 2.2.1. Ligne équipotentielle Définition Une ligne équipotentielle correspond à l’ensemble des points ayant le même potentiel. Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 2 sur 6 Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Page 3 sur 6 Remarque : Si A et B appartiennent à la même surface équipotentielle alors VA = VB Soit VA - VB = 0 D’où E . AB = 0 par conséquent E perpendiculaire à AB Les surfaces équipotentielles sont perpendiculaires aux lignes de champ. Topographie des lignes équipotentielles S d N - + E E - E d ’ E - 0V P 1,5 V 3V 4,5 V + + + + 6V 2.2.2. Relation entre champ électrostatique et tension Dans le cas particulier où A et B appartiennent respectivement aux plaques P et N, on a: VP – VN = Ed On en déduit une expression de la norme E : Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 3 sur 6 Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Page 4 sur 6 E = Error! = Error! = Error! avec U tension entre les armatures et d la distance séparant les armatures. 2.2.3. Autre expression du travail de la force électrostatique W ( Error!) = q Error!. Error! or Error!. Error! = VA – VB W ( Error!) = q. (VA – VB) = q UAB Remarques : - Si q > 0, Error! et Error! ont le même sens, une charge positive descend les potentiels. - Si q< 0, Error! et Error! sont de sens contraires, Une charge négative remonte les potentiels. - La travail de la force électrostatique peut également s’exprimer en électron-volt (eV) 1eV = 1,6.10-19J 3. Energie potentielle électrostatique 3.1. Expression de l’énergie potentielle électrostatique Le travail de la force électrostatique est : (VA- VB) =qVA - qVB W (F ) = q Posons EpA = EpB q VA : énergie potentielle électrostatique en A = q VB : énergie potentielle électrostatique en B. Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 4 sur 6 Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Page 5 sur 6 De façon générale l’énergie potentielle électrostatique est : E P = q.(V-V0) où V0 est le potentiel à l’état de référence. 3.2. Variation de l’énergie potentielle Soit une charge q passant d’un point P au potentiel V P à un point N de potentiel VN sous l’action de la force électrostatique F W ( F ) = q (VP- VN) = q VP - q VN = E - E PP PN W ( F ) = - ΔΕP 3.3. Conservation de l’énergie Soit une particule de masse m et de charge q (q> 0) se déplaçant sans frottement dans un champ électrostatique E A VA – VB E F B Système : la particule Bilan des forces : - La force électrostatique Error!= q. Error! Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 5 sur 6 Phase d’acquisition (Classe 1ère D, Année 2014-2015) – OG 3- Chap. 6: Energie potentielle électrostatique Page 6 sur 6 - Le poids Error! de la particule (le poids est négligeable devant la force électrostatique). Théorème de l’énergie cinétique : E C (B) – E C (A) = WAB (F) E C (B) – E C (A) = q. (VA – VB) EC (B) + qVB = EC (A) + EC (A) EA=EB v2 E = Error!m + qV : Energie totale de la particule chargée dans le champ électrostatique. L’énergie totale d’une particule se conserve. 4. Le principe de l’oscilloscope Circuit de chauffage Filament Anode Cathode E e + HT - Canon à électrons Première D - Physique – Chap. 6 Energie potentielle électrostatique Page 6 sur 6