Mouvements d`un solide

1ère S TP physique 02
Mouvements d’un solide
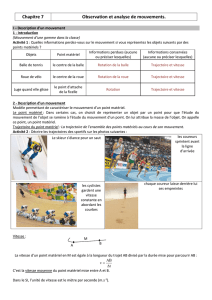
Etude des mouvements de la maquette d’une grande roue et d’une de ses nacelles.
Ensemble. Réalisation du document vidéo à
l’aide d’une webcam et du logiciel
« Généris ».
Enregistrement au format « .avi » sous le
nom « rotation.avi », à l’adresse « 1Sb \
documents » sur le réseau.
Par groupes. Traitement des mesures avec le
logiciel « Aviméca ». Se référer à la notice
d’utilisation.
 Lancer l’application. Ouvrir le fichier
« rotation.avi ». Adapter sa dimension, à
l’aide de l’icône « % » de la barre d’outils.
 Dans le menu « propriétés du clip », noter la fréquence des images et la durée entre deux
prises de vue. Comment, par calcul, l’une peut-elle se déduire de l’autre ?
 Dans le menu « étalonnage », préciser l’échelle du document : se référer au document ci-
dessus où la distance entre les deux axes de nacelles est L = 27,0 cm.
Régler à 2 le nombre de points par image. Choisir pour chaque point une forme de marquage
différente.
 Choisir également, dans la barre d’outils, une dimension de points égale à 3. Choisir la
couleur blanche pour le pointeur.
 Choisir la première image qui permettra de repérer les positions successives de la nacelle
bleue munie de pastilles jaunes. Prendre l’origine des dates sur cette image.
Enregistrement. Matérialiser sur l’écran les positions successives du centre de chacune des
pastilles de la nacelle bleue, jusqu’à ce que leurs trajectoires se croisent.
Prendre ensuite le relais avec les pastilles orange et jaune situées sur les barres de roue,
pendant environ un demi-tour.
.
 Dans le menu imprimer, configurer l’imprimante en mode « paysage », définir la zone
d’impression (si possible, une échelle simple). Quand l’imprimante est libre, imprimer.
Exploitation.
Au fur et à mesure des questions, on pourra se référer à la notice en fin de document, concernant
les définitions de vitesses.
Mouvement de la roue.
1. Appelons A et B chacun des points mobiles de la roue. Ils sont situés à 9,0 cm et 16,0 cm du
centre du disque. Vérifier que chaque trajectoire est circulaire, de centre O à déterminer. Mesurer
les rayons, vérifier et éventuellement corriger l’échelle du document.
2. Le mouvement de chaque point paraît-il uniforme ? Justifier.
3. Repérer 3 positions qui se correspondent (c’est-à-dire aux mêmes dates) des deux points
mobiles :
 Déterminer vitesses linéaires (attention à l’échelle du document) et vitesses angulaires.

1ère S TP physique 02
 Commenter les résultats obtenus :
- pour chaque point mobile, vitesse linéaire et vitesse angulaire restent-elles constantes ?
- les deux points mobiles ont-ils même vitesse angulaire ? même vitesse linéaire ?
 De quoi dépend la vitesse linéaire ? La relation théorique entre vitesse linéaire et vitesse
angulaire est-elle vérifiée ?
 A partir de la valeur de , déterminer la fréquence de rotation en Hz, puis en tours par
minute.
4. Tracer les vecteurs vitesses (tenir compte du fait que la trajectoire est circulaire). Préciser
l’échelle (convenable) choisie.
 Le vecteur vitesse est-il constant au cours du mouvement d’un point ? Expliquer.
Mouvement de la nacelle.
1. Appelons C et D chacun des points mobiles. Vérifier que chaque trajectoire est circulaire,
déterminer avec précision son centre et son rayon. Observation.
2. Repérer 3 positions qui se correspondent de chacun des points mobiles C et D. Tracer les 3
segments CD. Remarques.
3. Pour chaque point, déterminer les vitesses linéaires et représenter les vecteurs vitesses.
Observations.
Conclusion.
Le mouvement du disque est un mouvement de rotation, celui de la nacelle un mouvement de
translation circulaire. Faire ressortir ressemblances et différences.
________________________________________________________________________________
Définitions.
1. Le vecteur-vitesse.
La vitesse du mobile étant déterminée à une date donnée t, on définit le vecteur-vitesse
v
de la
manière suivante (voir schémas) :
- origine : la position M du mobile à la date t.
- direction : la trajectoire du mobile si le mouvement est
rectiligne,
la tangente à la trajectoire si le mouvement est
curviligne.
- sens : celui du mouvement.
- norme : proportionnelle à la valeur de la vitesse (choix d’une
échelle).
On peut en première approximation dire que la vitesse du mobile à la date t est
't"t "M'M
v 
, que
l’on écrit encore
t"M'M
v 
, t’ et t’’ étant deux dates entourant immédiatement t.
2. Le mouvement circulaire uniforme.
On note l la mesure de l’arc MM’, t la durée du trajet de M vers M’.
est la mesure de l’angle (
OM
,
'OM
) balayé par le « rayon-
vecteur » au cours du mouvement.
 La relation entre ces deux grandeurs est l = R. , R étant le rayon du
cercle et l’angle étant exprimé en radians (rad). On rappelle qu’un
tour correspond à 2 radians (360°).
 La vitesse linéaire du point mobile est
Δt
l
v 
et la vitesse angulaire
Δt
α
ω
. Unités.
 Entre vitesse linéaire et vitesse angulaire, il existe la relation v = R. .
 Le mouvement est périodique de période T, durée d’un tour. La fréquence f est le nombre
de tours effectué par unité de temps :
T
1
f 
. Si T est en s, f est en Hz ou tr.s-1.
M
M’
l
O
R
v
M
v
M’
M’’
M