Baccalauréat S Physique-Chimie Amérique du Nord 2015 (extrait

Documents de Physique-Chimie-M. MORIN
Baccalauréat S Physique-Chimie Amérique du Nord 2015 (extrait).
Bac Panther
Super héros en danger.
2. Problème technique.
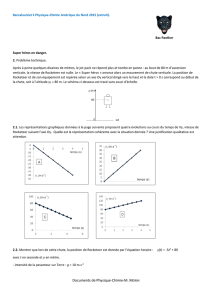
Après à peine quelques dizaines de mètres, le jet-pack ne répond plus et tombe en panne : au bout de 80 m d’ascension
verticale, la vitesse de Rocketeer est nulle. Le « Super héros » amorce alors un mouvement de chute verticale. La position de
Rocketeer et de son équipement est repérée selon un axe Oy vertical dirigé vers le haut et la date t = 0 s correspond au début de
la chute, soit à l’altitude y0 = 80 m. Le schéma ci-dessous est tracé sans souci d’échelle.
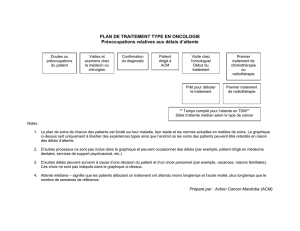
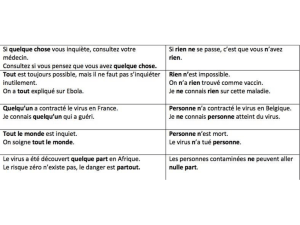
2.1. Les représentations graphiques données à la page suivante proposent quatre évolutions au cours du temps de Vy, vitesse de
Rocketeer suivant l’axe Oy. Quelle est la représentation cohérente avec la situation donnée ? Une justification qualitative est
attendue.
2.2. Montrer que lors de cette chute, la position de Rocketeer est donnée par l’équation horaire : y(t) = -5t2 + 80
avec t en seconde et y en mètre.
- intensité de la pesanteur sur Terre : g = 10 m.s-2

Documents de Physique-Chimie-M. MORIN
2.1.
Astuce : Repérer si la vitesse est nulle sur les graphiques. (Au début Rocketeer a une vitesse nulle)
On conserve les graphiques A et B, où la vitesse initiale est nulle.
Astuce : La vitesse prend des valeurs positives si le système se déplace dans le sens de l’axe.
La vitesse prend des valeurs négatives si le système se déplace dans le sens opposé à l’axe.
Dans ce cas, Rocketeer chute verticalement vers le bas. Le vecteur vitesse vitesse est dirigé vers le bas, tandis que l’axe Oy est
dirigé vers le haut alors les valeurs prises par les vitesses de Rocketeer seront négatives.
Le graphique A représente donc la situation de chute de Rocketeer.
Chemin de résolution (2.2.)
Référentiel : terrestre
Système : Rocketeer Application de la deuxième loi de Newton
Bilan des forces : 
 = 
Conditions initiales
Projection sur les axes Primitive Primitive
  (ax = 0 ; ay = -g)  (vx = 0 ; vy = -gt) 
(x = 0 ; y = 
)
Référentiel : Terrestre supposé galiléen
Système : Rocketeer
Bilan des forces : Le poids  (direction : verticale ; sens ; vers le bas ; norme : P = m.g)
Conditions initiales :
 (x0 = 0 ; y0 = 80 m) 
(v0x = 0 ; v0y = 0)
Application de la deuxième loi de Newton :

Documents de Physique-Chimie-M. MORIN
Par projection sur les axes :
Attention : Il faut toujours observer le sens des axes. On remarque ici, que l’axe vertical est dirigé vers le haut
tandis que le vecteur  est dirigé vers le bas d’où l’introduction d’un signe négatif.
 (ax = 0 ; ay = -g)
Quelle est la fonction du temps v(t) qui, dérivée une fois par rapport au temps t, donne une constante -g ?
En calculant la primitive une première fois.
 (vx = 0 ; vy = -gt) avec v0x = 0 et v0y = 0
Quelle est la fonction du temps OG(t) qui, dérivée une fois par rapport au temps t, donne une fonction du premier degré de t
(v(t) ?
En calculant la primitive une seconde fois.
(x = 0 ; y = 
 ) avec x = 0 et y0 = 80 m.
On en déduit que :
y = 