Fonctions Continues et le Théorème des Valeurs Intermédiaires 1

Université Paris Est Créteil
DAEU
TD 11 : Fonctions Continues et le Théorème des Valeurs
Intermédiaires
Dans cette fiche on définie une propriété très importante qui est vérifiée par un très grand
nombre de fonctions : la continuité.
On énonce et on utilise un théorème sacrément intuitif.
1 Representation graphique
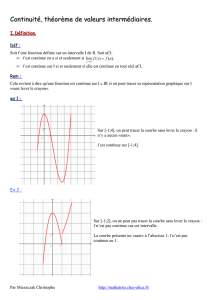
Exercice 1 On se donne la fonction fdéfinie sur l’intervalle [−3,8] dont la représentation graphique
est donnée ci dessous.
1
2
3
4
5
12345678−1−2−3
•
•
•
•
1. Déterminer les images de −3,−2,0,2et 6par f.
Par lecture graphique on a
f(−3) = 5 ; f(−2) = 4 ; f(0) = 3 ; f(2) = 3 ; f(6) = 3
2. Déterminer l’expression de f(x)pour x∈[−3,8].
Le graphe de fest constitué uniquement de segments donc pour chacun des segments on a une
expression du type f(x) = ax +b. On a facilement :
f(x) =
−x+ 2 si x∈[−3,−1]
3si x∈[−1,2]
4si x∈]2,4]
x
2+ 2 si x∈[4,6[
3si x= 6
−x
2+ 5 si x∈]6,8]
3. Par lecture graphique, déterminer
1

(a) lim
x→−3
x>−3
f(x)= 5
(b) lim
x→1f(x)= 3
(c) lim
x→2
x<2
f(x)= 3
(d) lim
x→2
x>2
f(x)= 4
(e) lim
x→6
x<6
f(x)= 5
(f) lim
x→6
x>6
f(x)= 2
4. ⋆Que peut-on dire de lim
x→−3
x<−3
f(x)et de lim
x→8
x>8
f(x)?
C’est limites n’ont aucun sens car la fonction fn’est pas définie pour x < −3ou bien x > 8.
2 Les fonctions continues
2.1 Définitions et exemples
Dans toute cette section ("2 Les fonctions continues") on travail sur un intervalle quelconque qui
contient au moins deux éléments, cette intervalle sera noté I.
C’est à dire :
•Iest un intervalle borné : pour a, b ∈Rtels que a < b
I= [a, b]ou bien I=]a, b]ou bien I= [a, b[ou bien I=]a, b[
ou bien
•Iest un intervalle non-borné (avec c∈R) :
I=]c, +∞[ou bien I= [c, +∞[ou bien I=] − ∞, c]ou bien I=] − ∞, c[ou bien I=R.
On dit qu’une fonction fdéfinie sur un intervalle Iest continue lorsque pour tout x0∈Ion a
lim
x→x0
f(x) = f(x0),
c’est à dire
•limx→x0f(x)existe
•cette limite vaut f(x0)
Cette définition peut sembler bien étrange à première vu ... Par contre une interprétation graphique
simple peut-être faite :
Une fonction fdéfinie sur un intervalle Iest continue lorsque l’on peut
tracer sa représentation graphique sans lever le stylo.
Si une fonction n’est pas continue, on dit qu’elle est discontinue ; moralement on peut visualiser une
telle fonction comme présentant des sauts (voir le graphe de l’exercice 1 aux points x= 2 et x= 6).
2

Exercice 2
1. Soit
f: [0,2] →R
x7→ (1si x∈[0,1]
2si x∈]1,2] .
a. Dans le graphique ci-contre tracer la
courbe représentative de la fonction fsur
l’intervalle [0,2].
b. La continuité par le graphique.
En observant la représentation graphique
de la fonction f, selon vous, fest-elle
continue ?
c. La continuité par le calcul.
Calculer limx→1
x>1
f(x). La fonction fest-
elle continue dans [0,2] ?
1
2
1 2
Exemple. Les fonctions usuelles sont continues sur tout intervalle inclus dans leur domaine de défi-
nition :
0
1
2
-1
-2
1 2-1-2
0
1
2
3
4
1-1-2
0
1
2
3
4
-1
-2
-3
-4
-5
1 2 3-1-2-3-4
0
1
2
3
4
1-1-2
f(x) = xest continue
sur R
f(x) = x2est continue
sur R
f(x) = 1
xest continue
sur ]− ∞,0[ et ]0,∞[
f(x) = exest continue
sur R
Remarques. Le fait que les fonctions usuelles soient continue sur leur ensemble de définition permet
de justifier les calculs du type
lim
x→1x2−5 = −4ou bien lim x→−57
1
x−x=−1 57 + 57.
Par contre cela ne dit rien pour des limites intéressantes, i.e. pour des limites sur le bord du domaine
de définition.
Exemple. On peut facilement construire des fonctions qui sont discontinues :
3

0
1
2
-1
-2
1-1-2 •
0
1
2
3
4
1 2 3 4
•
f(x) = 
−1si x∈[−2,0[
0si x= 0
1si x∈]0,2]
est discontinue
On observe un saut en x= 0
La fonction partie entière définie par x7→ f(x)
où f(x)est l’entier qui est immédiatement
inférieur ou égal à x
Cette fonction est définie sur Ret est discontinue :
on observe des sauts en chaque valeures entières de x
On peut montrer la proposition suivante [voir Exercice 3]
Proposition. Soit fune fonction définie sur un intervalle I. Si fest dérivable sur Ialors fest continue
sur I.
Exercice 3 ⋆Démontrer la proposition précédente.
Remarque. Attention la réciproque à la proposition précédente est fausse : il existe des fonctions
continues qui ne sont pas dérivables. [Voir Exercice 4]
Exercice 4 ⋆On a déjà rencontrer la fonction valeur absolue qui a x∈Rassocie la valeur absolue
de xnotée "|x|" où
|x|=(xsi x≥0
−xsi x≤0.
1. Tracer le graphe de la fonction valeur absolue pour x∈[−5,5].
2. Pourquoi la fonction valeur absolue est-elle continue sur [−5,5] ? [Utiliser le graphique]
3. Montrer que |x|n’est pas dérivable en 0.
4

2.2 Le Théorème des Valeurs Intermédiaires
On travail dans cette section sur un intervalle fermée et bornée : I= [a, b]où a, b ∈Ret a < b.
On se donne une fonction fdéfinie et continue sur [a, b].
Définition. On dit que ℓ∈Rest une valeur comprise entre f(a)et f(b)lorsque
f(a)≤ℓ≤f(b)si f(a)≤f(b)
ou bien
f(a)≥ℓ≥f(b)si f(a)> f(b)
.
Le Théorème des Valeurs Intermédiaires (abrégé par TVI et énoncé ci-dessous) exprime un fait presque
évident :
•on fixe une valeur ℓcomprise entre f(a)et f(b)
•Le but du TVI est de prouver l’existence d’une solution à l’équation f(x) = ℓoù l’inconnue est
xet xparcourt l’intervalle [a, b].
L’existence d’une telle solution est affreusement évidente sur un graphique, cela se fait en 3 étapes :
1) On trace la courbe C
de la fonction f
2) On place ℓsur les ordonnées
On trace la droite y=ℓ
(ici en pointillés)
3) Le théorème dit :
il existe x0∈[a, b]tel que
le point (x0, ℓ)soit sur la courbe
C
]
b
[
a
•
•f(a)
f(b)
C
]
b
[
a
•
•–f(a)
f(b)–
-
ℓ
C
]
b
[
a
•
•–f(a)
f(b)–
-
ℓ•
|
x0
Plus précisément, le théorème peut s’énoncer de la manière suivante :
Théorème des Valeurs Intermédiaires [TVI].
Soit fune fonction continue sur un intervalle [a, b]et soit ℓune valeur comprise entre f(a)et f(b),
alors il existe x0∈[a, b]tel que f(x0) = ℓ.
Remarque.
1. Ce théorème peut se reformuler de la manière suivante :
Toutes les valeurs comprises entre f(a)et f(b)sont atteintes au moins une fois par f.
2. Le TVI ne donne aucune information sur la localisation de la solution x0outre le fait que
x0∈[a, b].
Généralement, si on désire une valeur approché de cette solution, alors on procède par dichotomie
en divisant l’intervalle [a, b]en sous intervalle et on essaie alors de localiser quel sous intervalle
contient une solution en réitérant l’utilisation du TVI.
3. Le TVI ne donne aucune information sur le nombre de solution outre le fait que l’on sait
qu’il en existe au moins une.
Par contre, si on sait que la fonction fest strictement monotone (strictement croissante ou bien
strictement décroissante) alors, il est clair que l’équation f(x) = ℓpossède au plus une solution.
Ainsi si x0est une solution, alors x0est unique.
4. L’hypothèse "fest continue sur [a, b]" est fondamentale. Par exemple avec a=−3et b= 8,
la fonction de l’exercice 1 est définie sur [−3,8] mais n’est pas continue. On a f(−3) = 5 et
f(8) = 1 par contre, on peut facilement voir qu’il n’existe pas de x∈[−3,8] tel que f(x) = 5/2
et pourtant 1≤5/2≤5...
5