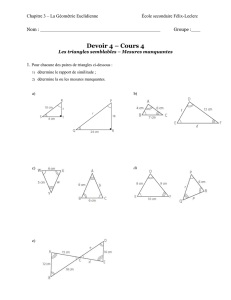
Exercice n°1 On considère un parallélogramme ABCD tel que AB=5

Géométrie – Seconde – 2799 – Triangles semblables démonstrations – 21.04.12 http://www.soutienpedagogique.com
Exercice n°1
On considère un parallélogramme ABCD tel que AB=5 cm et AD=3 cm. La bissectrice de l’angle BAD coupe (DC) en
M et (BC) en N. Démontrer que les triangles ADM et ABN sont isocèles et semblables. Calculer le ratio 
.
Exercice n°2
Démontrer que dans la figure suivante les triangles AMQ et APN sont semblables. En déduire l’égalité 
. Démontrer l’égalité suivante où R désigne le rayon du cercle : .
Application : dans la figure ci-dessous, calculer AM sachant que ABCD a pour côté 6 cm.
Exercice n°3
On considère le triangle ABC ci-dessous tel que AB = 28 mm, BC = 39 mm et AC = 42 mm. On note I le milieu du
segment  et D le point tel que 
. Démontrer que les triangles AID et ABC sont semblables.
Calculer la longueur ID.

Géométrie – Seconde – 2799 – Triangles semblables démonstrations – 21.04.12 http://www.soutienpedagogique.com
Exercice n°1
Démontrons tout d’abord que le triangle ADM est isocèle.
Comme la droite (AN) est la bissectrice l’angle
, on a: 
.
Comme ABCD est un parallélogramme, les droites (AB) et (DC) sont parallèles. 
 et   sont donc
des angles alternes-internes et on a : 
.
Démontrons que les triangles ADM et ABN sont semblables.
Comme ABCD est un parallélogramme, on a 
.
Démontrons enfin que ABN est isocèle.
Comme les triangles ADM et ABN sont semblables et que ADM est isocèle en D, alors :
.
On a AB=5 cm et AD=3 cm.
On passe des longueurs des côtés du triangle ABN aux longueurs des côtés du triangle ADM avec un coefficient de
réduction de 
. D’après le cours, on passe donc de l’aire du triangle ABN à l’aire du triangle ADM avec un
coefficient de réduction de 
 :
Exercice n°2

Géométrie – Seconde – 2799 – Triangles semblables démonstrations – 21.04.12 http://www.soutienpedagogique.com
Démontrons que AMQ et APN sont semblables.
Comme P appartient à la droite (AQ) et N appartient à la droite (AN), on a évidemment : 
.
Comme les quatre points M, N, P et Q appartiennent au cercle, l’angle 
 et l’angle 
sont deux
angles inscrits qui interceptent le même arc 
. On a donc 
.
Déduisons-en l’égalité .
Démontrons l’égalité suivante où R désigne le rayon du cercle : .
On voit sur la figure que :  .
Calculons la longueur AM de la deuxième figure, sachant que ABCD a pour côté 6 cm.
On a d’après la question précédente : . Calculons donc : 
R est égal à la moitié du diamètre du cercle qui est clairement égal au côté du carré ABCD : 
On utilise le théorème de Pythagore sur le triangle ADC pour calculer AC et en déduire AO :

Géométrie – Seconde – 2799 – Triangles semblables démonstrations – 21.04.12 http://www.soutienpedagogique.com
On utilise le théorème de Pythagore sur le triangle  pour calculer  :
On peut aisément démontrer que est le milieu de  en se rappelant que est perpendiculaire à
(DC) par définition d’une tangente à un cercle.  est donc parallèle à (AD) puisque 
 est un angle
droit, et la distance entre  et (AD) est égale à 3 et également à .
Exercice n°3
On considère le triangle ABC ci-dessous tel que AB = 28 mm, BC = 39 mm et AC = 42 mm.
Démontrons que les triangles AID et ABC sont semblables.
On a 
 d’après l’énoncé.Comme P appartient à la droite (AB) et D appartient à la droite (AC),
on a évidemment : 
.
Déduisons-en la longueur ID :