découverte: sinus et tangente d`un angle

CHAPITRE 4
DÉCOUVERTE: SINUS ET TANGENTE D’UN ANGLE
40°
O
A1
B1x
y
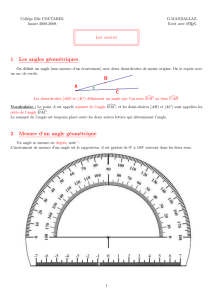
Sur la figure ci-dessus, les demi-droites [Ox) et [O y) forment un angle de mesure 40◦. Le point A1est sur
[O y), et le point B1est le projeté orthogonal de A1sur [Ox).
1. Commencez par placer quatre points A2,A3,A4et A5un peu au hasard sur la demi-droite [O y), puis
placez leurs projetés orthogonaux sur la demi-droite [Ox) (B2,B3,B4et B5respectivement). Soyez
précis !
2. Complétez le tableau suivant : vous mesurerez les longueurs directement à la règle graduée sur la
figure, et calculerez les quotients à l’aide de votre calculatrice (en arrondissant les résultats au cen-
tième)
OAiOBiAiBi
OBi
OAi
AiBi
OAi
AiBi
OBi
Pour i=1
Pour i=2
Pour i=3
Pour i=4
Pour i=5
3. Que pensez-vous des résultats obtenus sur la quatrième colonne ? Pouvez-vous les expliquer ?
4. Il est manifeste que les rapports OBi
O Aipour i=1,2,3,4,5 sont égaux, et la valeur de ce rapport ne
dépend que de l’angle entre les demi-droites [Ox) et [O y) (voir page suivante). Ces rapports sont
égaux à un nombre que l’on appelle cosinus de l’angle xO y . On l’obtient à la calculatrice à l’aide
de la touche cos . A la calculatrice, donnez la valeur arrondie au millième de cos 40◦≃......... et
comparez aux quotients que vous avez trouvés dans la quatrième colonne du tableau.
3ème Page 1/2 Activité de découverte

Voici maintenant une autre figure, presque identique à la première, si ce n’est que l’angle entre les deux
demi-droites vaut maintenant 28◦:
28°
y
x
O
A1
B1
1. Comme précédemment, placez quatre points A2,A3,A4et A5un peu au hasard sur la demi-droite
[O y), puis placez leurs projetés orthogonaux sur la demi-droite [Ox) (B2,B3,B4et B5respectivement),
et complétez soigneusement le tableau suivant :
OAiOBiAiBi
OBi
OAi
AiBi
OAi
AiBi
OBi
Pour i=1
Pour i=2
Pour i=3
Pour i=4
Pour i=5
2. On peut constater, comme précédemment, que les rapports de la quatrième colonne sont (presque)
égaux entre eux, et que la valeur de ces rapports est différente de ceux obtenus précédemment.
Comme seul l’angle formé par les deux demi-droites a changé, c’est que la valeur de ces rapports
ne dépend que de la mesure de cet angle ; ces rapports sont égaux au cosinus de l’angle de mesure
28◦, qui vaut (à la calculatrice) cos28◦≃.........
3. Que pensez-vous des résultats obtenus dans les deux dernières colonnes ?
4. Pour chacune des deux configurations, il est manifeste que les rapports AiBi
O Aipour i=1,2,3,4,5 sont
égaux, et la valeur de ce rapport ne dépend que de l’angle entre les demi-droites [Ox) et [O y). Ces
rapports sont égaux à un nombre que l’on appelle sinus de l’angle xO y . On l’obtient à la calculatrice
à l’aide de la touche sin . A la calculatrice, donnez la valeur arrondie au millième de sin40◦≃.........
et de sin28◦≃.........
5. Pour chacune des deux configurations, il est tout aussi manifeste que les rapports AiBi
OBipour i=
1,2,3,4,5 sont égaux, et la valeur de ce rapport ne dépend que de l’angle entre les demi-droites [Ox)
et [O y). Ces rapports sont égaux à un nombre que l’on appelle tangente de l’angle xO y . On l’obtient
à la calculatrice à l’aide de la touche tan . A la calculatrice, donnez la valeur arrondie au millième de
tan40◦≃...... ... et de tan28◦≃.........
3ème Page 2/2 Activité de découverte