POLY-PREPAS Centre de Préparation aux Concours - Poly

1
POLY-PREPAS
Centre de Préparation aux Concours Paramédicaux
- Section i-Prépa -

2
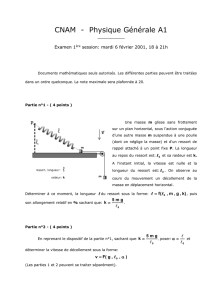
exercice 1 : Pendule élastique horizontal
Un solide de masse m = 165 g est attaché à l’extrémité d’un ressort dont l’autre extrémité A est fixe.
L’axe de symétrie du ressort est horizontal et le solide peut glisser le long d’une tige horizontal D sans
frottement appréciable. La tige D est confondue avec l’axe de symétrie du ressort. La constante de
raideur du ressort est k = 13,2 N.m-1. On désigne par O la position du centre d’inertie G du solide à
l’équilibre sur la droite horizontale D et par i un vecteur unitaire de cette droite orientée de A vers G.
1. Le solide étant immobile, on l’écarte de se position d’équilibre d’une longueur
xm = 45mm. A un instant donné pris comme origine du temps, on lâche le solide.
Etablir l’équation différentielle qui régit le mouvement du centre d’inertie G du solide.
2. Dans le repère [O ; i), l’équation différentielle trouvée admet des solutions de la forme :
x = xm cos[ (2p/T0) t + f]
a) déterminer l’expression de la période propre T0 de l’oscillateur
b) vérifier que l’expression trouvée est homogène à un temps par une analyse
dimensionnelle
c) calculer la période propre T0 du pendule élastique
3. Déterminer précisément l’équation horaire du mouvement de G le long de l’axe [O ; j)
(c-à-d déterminer numériquement xm, 2
p /T0, et f)
4. Déterminer au cours du mouvement :
a) la vitesse maximale de S
b) l’accélération maximale de S
5. a) Définir et exprimer l'énergie mécanique de cet oscillateur non amorti.
b) Calculer sa valeur à l'instant t = 0. (On prendra l'énergie potentielle du ressort nulle
lorsque x = 0).
c) En admettant et en utilisant la conservation de cette énergie mécanique, retrouver la valeur
maximale de la vitesse du solide
exercice 2 :
Partie A
Un pendule élastique est constitué d’un ressort à spires non jointives, de constante de raideur K = 40
N.m-1, d’axe horizontal et de masse négligeable. L’une de ses extrémités est fixée à un support
immobile. À l’autre extrémité est accroché un solide de masse m = 100 g pouvant osciller librement
selon l’axe horizontal Ox (voir figure 1 )

3
En position d’équilibre le centre de gravité G de ce solide coïncide avec l’origine O de l’axe
horizontal, orienté positivement vers la droite (voir figure 1)
Le solide est écarté de sa position d’équilibre de sorte que l’abscisse de son centre de gravité G soit de
+ 5,0 cm (figure 2).
À l’instant t = 0, il est lâché sans vitesse initiale et son mouvement est enregistré (figure 3)
Les forces de frottement ainsi que l’amortissement du mouvement sont considérés comme
négligeables. L’intensité de la pesanteur est g = 10 N.kg-1.
On désigne par T0 la période propre des oscillations.
Figure 1
5 cm x
support
plan
Figure 2
O
y
G
G

4
Toutes les valeurs demandées dans l’exercice devront être exprimées dans les unités du Système
international (S.I.) Ces unités devront être précisées.
1. Faire l’inventaire des forces extérieures appliquées sur le solide immédiatement après le
lâcher ; les représenter
2. L’équation différentielle du mouvement de G peut s’écrire:
&&
X
+
K
m
X = 0 où X est l’abscisse
de G à la date t.
a) Montrer que X(t) = Xm cos
0
2
T
p
t est solution de l’équation différentielle du
mouvement à condition d’exprimer T0 en fonction de K et m.
b) En utilisant les conditions initiales, donner la valeur de Xm .
3. Période.
a) En utilisant les valeurs de m et de K, calculer la valeur de T0.
b) Cette valeur est-elle en accord avec celle que l’on peut déduire de la figure 3?
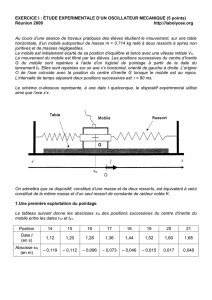
Partie B
En travaux pratiques, un montage quelque peu différent de celui de la figure 1 est réalisé : sur une
table à coussin d’air, on utilise 2 ressorts au lieu d’un seul (voir figure 4).
L’enregistrement du mouvement est donné en figure 5 ; il a été réalisé avec les valeurs suivantes :
K1 = 10 N.m-1, K2 = 20 N.m-1 et m = 100 g.
On montre que ce système à une masse et deux ressorts est équivalent à celui constitué de la même
masse et d’un seul ressort de constante de raideur Keq.
1. Quel est l’intérêt pratique d’utiliser deux ressorts au lieu d’un ?
2. En utilisant le graphique de la figure 5, montrer que Keq vérifie la relation Keq = K1 + K2.
3. Proposer une méthode permettant de déterminer la valeur d’une masse en état
d’impesanteur.
K1 K2
G
Figure 4

5
exercice 3 : Equation horaire
Un solide de masse m = 0,20 kg est mobile sur un banc à coussin d’air horizontal. Il oscille sous
l’action de deux ressorts, équivalents à un ressort unique de constante de raideur k = 5,0 N.m-1.
Les abscisses sont repérées sur un axe de même direction que les ressorts.
L’origine des abscisses est la position du centre d’inertie du solide lorsque celui-ci est au repos.
L’origine des dates correspond au passage du mobile par l’origine des abscisses avec une vitesse de
valeur 0,60 m.s-1 dirigée dans le sens négatif de l’axe.
Plusieurs équations horaires sont proposées pour décrire le mouvement du centre d’inertie du solide ;
en justifiant le choix, préciser quelle est la bonne :
a) x(t) = 0,06 cos (5t)
b) x(t) = 0,12 cos (5t)
c) x(t) = 0,06 cos (5t – p/2)
d) x(t) = 0,12 cos (5t + p/2)
e) x(t) = 0,012 cos (5t – p/2)