consulter le document - Kademia.tn Cours en ligne, Collège

1
Les oscillations libres d’un pendule élastique
Oscillations libres non amorties
Série d’exercices corrigés
Exercice 1 :
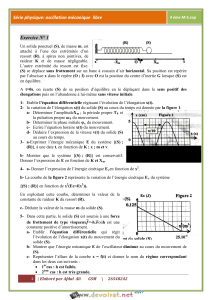
On considère l'oscillateur horizontal (Figure 1) constitué par un ressort de raideur
K auquel est accroché un corps (C) supposé ponctuel de masse m = 100g.
Lorsque C est en équilibre, son centre d’inertie G se trouve sur la verticale du
point 0 et le ressort n’est ni allongé ni comprimé.
On écarte le corps (C) de sa position d'équilibre (d'abscisse x = 0) et on le lâche
sans vitesse initiale à t = 0.
1- Etablir l'équation différentielle du mouvement du centre d’inertie G du
corps (C).
2- L'enregistrement du mouvement de (C) donne la courbe x = f (t).
figure 2

2
a- Ecrire l'équation horaire du mouvement de (C), en précisant
l'amplitude Xm, la pulsation propre ω0 et la phase initiale ϕx
b- Calculer la valeur de la constante de raideur K du ressort.
3-
a- Exprimer l'énergie mécanique E du système {corps (C), ressort} à
un instant t quelconque lorsque (C) passe une position d'abscisse x
à la vitesse v.
b- Déduire que l'énergie mécanique E du système est constante au
cours du mouvement.
Calculer sa valeur.
c- Exploiter la conservation de l'énergie pour montrer que
d- Avec quelle vitesse le corps (C) passe-t-il pour la première fois par
la position d'abscisse x = 2,4 cm?
4- On donne la courbe Ep = f (t), représentant l’énergie potentielle du
système (Figure 3).

3
a- Comparer la période T de l’énergie potentielle Ep à la période propre T0
de l’oscillateur.
b- Représenter clairement sur le document suivant les courbes Ec = f (t)
représentant l’énergie cinétique du corps C, et E = f (t) représentant
l'énergie mécanique E du système {corps(C), ressort}.Justifier

4
Exercice 2 :
Un ressort à spires no jointives de masse négligeable et de coefficient de raideur
k = 20 N.m-1 est disposé sur un plan horizontal, l’une de ses extrémités est fixe,
on accroche à l’autre extrémité un solide (S) de masse m = 0,2 Kg. Ce solide
peut se déplacer sans frottement le long d’un axe horizontal (x’x). A l’équilibre,
le centre d’inertie G du solide (S) coïncide avec l’origine O du repère R (O,
On allonge le ressort vers la droite, le point G occupe la position G0 telle que
   et à l’instant t = 0, on lâche le solide avec une vitesse
initiale v0 =0,25 ms-1.
1-
a- Etablir l’équation différentielle qui régit le mouvement de (G).
b- En déduire l’expression de la pulsation propre  des oscillations de
(G).
c- Vérifier que quelque soient les valeurs de Xm les valeurs et ,
l’équation horaire     est solution de l’équation
différentielle précédente.
2-
a- Déterminer la valeur de l’amplitude Xm et celle de la phase
initiale.
b- En déduire l’expression de la vitesse instantanée v(t) de solide (S)
en fonction de temps.
c- Trouver la date pour laquelle le solide passe par sa position
d’équilibre pour la 5ème fois.

5
3-
a- Donner l’expression de l’énergie mécanique de cet oscillateur.
b- Montrer que cette énergie se conserve au cours de temps.
c- En déduire son expression en fonction de K, m, x0 et v0. Calculer
sa valeur.
Exercice 3 :
Un solide (S) de masse m peut glisser, sans frottement, sur un plan horizontal.
Le solide est lié à l’une des extrémités d’un ressort (R) à spires non jointives de
masse négligeable et de raideur K. A l’origine des temps, on communique au
solide (S) pris dans sa position d’équilibre une vitesse initiale V0 = - 0,5 ms-1, il
se met alors à osciller de part et d’autre de sa position d’équilibre O origine du
repère (O,)
Au cours de son mouvement, le centre d’inertie G du solide est repéré par son
abscisse x(t).
1.
a- En appliquant la RFD, établir l’équation différentielle vérifiée par
l’abscisse x du solide et en déduire la nature du mouvement du solide.
b- Montrer que      est solution de l’équation
différentielle si 
c- Déterminer l’expression de la vitesse instantanée du solide v(t).