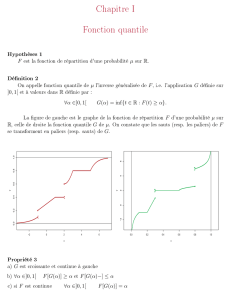
Fiche résumée du cours d`intégration et probabilités

σE
E∈E
A∈E⇒E−A∈EAC
(An)n∈N∈E∪
n∈NAn∈E
E
E
B(E)
A∈P(E)
A A
σ(A)
(E, E)
µE→[0,+∞]
µ(∅)=0
(An)n∈N
µ(t
n∈NAn) = X
n
µ(An)
µ(∪
n∈NAn)≤Pnµ(An)
A⊂B µ(A)<∞µ(B−A) = µ(B)−µ(A)
(An)n∈Nµ(∪
n∈NAn) = lim ↑µ(An)
(Bn)n∈Nµ(B0)<∞
µ(∩
n∈NBn) = lim ↓µ(Bn)
µ µ(E)<∞
µ µ(E)=1
µ σ (En)n∈N
∀n∈Nµ(En)
x∈E µ {x} ∈ Eµ({x})>0
µ
(E, E, µ)
δ(A) = 1{0∈A}
(An)n∈N
(E, A, µ)P
n≥1
µ(An)<∞
µ(lim sup
n→+∞
An) = 0 lim sup
n→+∞
An=T
n≥1S
k≥n
Ak
(E, E) (F, F)
f E →F∀B∈Ff−1(B)∈
Ef

(E, E, µ)
(fn)n∈Nf(E, E)R
(fn)n∈Nf∀ε
µ({|f−fn|> ε})→
n→∞ 0
F=σ(A)
AF f : (E, E)→(F, F)
∀A∈Af−1(A)∈EE F
f:E→F
f1f2x7→ (f1(x), f2(x))
E×F
(an)n∈N
(an)
(an)
lim sup an= lim
n→+∞↓sup
k≥n
(an) lim
n→+∞an
lim inf an= lim
n→+∞↑inf
k≥n(an) lim
n→+∞
an
lim anlim sup(an) = lim inf(an) = l
fnn∈NE→
Rsup
n
fn:x7→ sup
n
fn(x) inf
nfn:x7→ inf nfn(x) lim n→+∞sup(fn)
lim
n→+∞inf(fn){x∈E| ∃ lim n→+∞fn(x)∈R+}
M
E∈M
(A, B)∈M2A⊂B B −A∈M
(An)n∈N∈M M An⊂An+1∀n
∪
n∈NAn∈M
C
(Mi)C
∩Mi
C M (C)C
M(C) = σ(C)
µ ν (E, E)C
µ(A) = ν(A)∀A∈C C
µ ν µ(E) = ν(E)µ ν
σ(C)ν=µ σ(C) = E
(En)n∈NEµ(En) = ν(En)<∞
∪En=E µ ν σ(C)

f: (E, E)→R+
f f =Pn
i=1 αi.χAi0≤αi< ... < αn
f Ai={x∈E, f(x) = αi}
mRfdm =Pn
i=1 αi.m(Ai)
0∗ ∞ = 0 αi= 0 m(Ai) = ∞
f:E→
R+Rfdµ =sup{Rhdµ h 0≤h≤f}
(fn)n∈NE→R+
f∞= lim ↑fn
lim
n→+∞↑Zfndµ =Zlim n→+∞↑fndµ =Zf∞dµ .
f E →R+
∀a > 0, µ({x∈E, f(x)≥a})≤1
aRfdµ
Rfdµ < ∞µ({x∈E f(x) = ∞})=0 f
µ
{x, f(x)>0}Rfdµ = 0 f= 0 µ
fn:E→R+
lim inf(fn)
Rlim inf(fn)≤lim inf Rfndµ
f µ
R|f|dµ
L1(E, µ) = {f:E→RZ|f|dµ < ∞}
Rd
fn:E→
R
fn(x)→
n→∞ f(x)µ
∃g∈L+
1|fn(x)|≤ g(x)∀n µ
fnf∈L1R|fn−f|dµ →0Rfndµ
Rfdµ
(fn)n∈N
E→R+fn→f µ Rfdµ
Rfndµ Rfdµ R|fn−f|dµ →0
(E, E, µ)
(fn)n∈Nfn→f µ(dx)
∀ε > 0∃A, µ(A)< ε fn
f E −A
(U, d)
f:U×E→R
∀u∈U f(u, .)x→f(u, x)∈L1(µ)
µ(dx)f(., x)u→f(u, x)u0
∃g∈L+
1(µ)|f(u, x)|≤ g(x)µ(dx)∀u∈U
I(u) = REf(u, x)µ(dx)U→Ru0

u0∈I
f:I×E→R
∀u∈I f(u, .)x→f(u, x)∈L1(µ)
µ(dx)f(., x)u→f(u, x)u0
∂u(u0, x)
∃g∈L+
1(µ)|f(u, x)−f(u0, x)|≤ g(x)|u−u0|µ(dx)
∀u∈U
F(u) = REf(u, x)µ(dx)I→Ru0
F0(u0) = RE∂uf(u0, x)µ(dx)
f∈L1(R)
F:x7→ Zx
0
f(t)dt
λ−∂F (x) = f(x)λ(dx)
f∈L1(R)x∈R
Mf(x, r) = 1
λ(B(x, r)) ZB(x,r)|f|(t)dt
Mf(x) = sup
r>0
Mf(x, r)
L1(R)f:R→R
kfkL1
W(R)= sup
t>0
(λ{x, |f(x)|> t}.t)
kfkL1
W<∞f∈L1
W
f∈L1(R)Mf ∈
L1
WkMfkL1
W≤3kfkL1
Ω = n ∪
i=1B(xi, ri)Rr
Ω⊂ ∪
k≥0B(xik,3rik)
λ
∂F ∈L1F(x) = F(0) + Rx
0∂F (t)dt
F:R→R
∀ε > 0∃η > 0 ]α1, β1[...]αn, βn[
n
P
i=1|F(βi)−F(αi)|< η Pn
i=1|F(αi−βi)|< ε.
n
X
i=1|F(αi−βi|≤ ZD|∂F (t)|dt →
D0
D=∪]αi, βi[
∂F ∈L1
loc(R)F(x) =
F(0) + Rx
0∂F (t)dt .

E
µ∗P(E)→
[0,+∞]
µ∗(∅)=0
µ∗A⊂B⇒µ∗(A)≤µ∗(B)
σ(An)n∈N∈P(E)N
µ∗(∪
n∈NAn)≤X
n
µ∗(An)
µ∗
B∈M(µ∗)∀A∈P(E)µ∗(A) = µ∗(A∩
B) + µ∗(A∩Bc)
M(µ∗)
µ∗(B)=0
µ µ∗M(µ∗)
A⊂R
λ∗(A) = inf{P∞
i=1(bi−ai)|A⊂∞
∪
i=1 ]ai, bi[}
λ∗
B(R)⊂M(λ∗)
∀a≤b λ∗([a, b[) = b−a
λ∗B(R)M(λ∗)
RB(R)iii)
Rd
Rd
λ∗
d(A) = inf{∞
X
i=1|Pi|Pi∪Pi⊃A}
|P|=Qd
j=1(bj−aj)P=Qd j=1 ]aj, bj[
(E, E, µ)
N∈P(E)µ N ∈
NA∈EN⊂A µ(A)=0 E=E∨N=σ(E,N)
E N E ={A⊂E| ∃B, B0∈Eµ(B0−B) =
0B⊂A⊂B0}={A=B∪N|(B, N )∈(E,N)}
Eµ
µ(A) = µ(B)B∈EB⊂A A −B∈Nµ
E E µ
M(λ∗) = B(Rd)
∀A∈B(Rd)
λ(A) = inf{λ(θ)θ θ ⊃A}= sup{λ(F)F F ⊂A}
(E, d)B(E)
µ µ ∀A∈B(E)
µ(A) = inf{µ(θ)θ θ ⊃A}= sup{µ(F)F F ⊂A}