Angles et polygones réguliers Fiche d`exercices n° 4 Exercice 1

Angles et polygones réguliers Fiche d’exercices n° 4 3ème
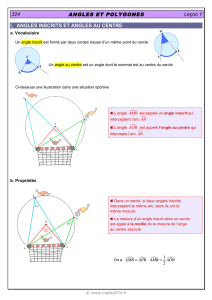
Exercice 1
Reproduire la figure ci-dessous avec GeoGebra.
Déplacer les points A,Bet C.
Que peut-on conjecturer ?
O
B
C
A
Exercice 2
Déterminer la mesure de l’angle E DC .
BC
D
E
29˚
Exercice 3
Une puce saute sur un cercle par bonds réguliers : c’est-à-dire que l’angle au centre formé par deux positions
consécutives de la puce est toujours le même. La puce va-t-elle pouvoir revenir à son point de départ si l’angle
fait 80° ?
Combien de tours aura-t-elle faits lorsqu’elle atteindra de nouveau le point de départ ?
Et si l’angle fait 60° ? S’il fait 70° ? Et 100° ? Et 40° ? Et 37° ?
Trouver tous les nombres pour lesquels la puce atteint de nouveau son point de départ en ayant effectué un
seul tour.
Trouver tous les nombres pour lesquels la puce atteint de nouveau son point de départ en ayant effectué deux
tours.
Exercice 4
Avec le logiciel GeoGebra, construire un cercle de rayon 2 cm, puis un ennéagone régulier (9 côtés) inscrit
dans ce cercle.
Page 1/2

Angles et polygones réguliers Fiche d’exercices n° 4 3ème
Exercice 5
Avec le logiciel GeoGebra :
1) tracer le cercle de centre Oet de rayon 1 ;
2) placer un point Asur ce cercle ;
3) créer un curseur nvariant de 3 à 100 avec un pas de 1 ;
4) avec le bouton (Angle de mesure donnée), placer un point sur le cercle tel que AOB =360°
n;
5) avec le bouton (Polygone régulier) tracer un polygone régulier de ncôtés dont Aet Bsont deux
sommets consécutifs, inscrit dans le cercle ;
6) avec le bouton (Distance ou Longueur) afficher la circonférence Ldu cercle et le périmètre Pdu
polygone régulier ;
7) déplacer le curseur et déterminer les valeurs de npour lesquelles L−P<0,001.
Exercice 6 Pour les rapides
O
B
C
K
M
[BC ] est un diamètre d’un cercle de centre O. Un point Kappartient à un demi-cercle d’extrémités Bet Cet
un point Mappartient à l’autre demi-cercle.
1) Réaliser cette figure avec GeoGebra.
2) Afficher les mesures des angles BOK et K MC .
3) Afficher la fenêtre tableur. Enregistrer dans le tableur les mesures des angles BOK et K MC (colonnes A et
B). Entrer dans la cellule C2 la somme
BOK
2
+ K MC . Déplacer le point K. Que peut-on constater ?
4) Démontrer cette conjecture.
Page 2/2