x - C2P1

!
Les extr@s sont un outil pédagogique vous permettant de revoir vos cours à
travers les points essentiels et les questions que vous vous posez le plus
couramment. Les explications sont dispensées par les RM et leur équipe.
Les extr@s sont une aide dans votre apprentissage voire compréhension des
différents cours, mais en aucun cas un substitut à vos cours magistraux ou TD.
Il vous est conseillé de consulter ce document après votre cours magistral afin
d’éclaircir les concepts les plus flous et vérifier votre assimilation des notions
de bases.
Si des questions persistent, n’hésitez pas à aller sur le forum :
http://www.ampcfusion.com
!
!
!
!
!
!
!
!
Cercle Cartésien des PAES – C2P1
Bureau T203 ∗ 45, rue des Saints-Pères 75006 Paris
Local TP15 ∗ 4, avenue de l’Observatoire 75006 Paris
01 42 86 40 59 ∗ [e-mail]
∗
http://c2p1.fr

Les!Extr@s!du!C2P1! BIOMATHS! n°1!INTÉGRATION!
!
!
2!
Intégration
I) Rappel sur l’intégration
Soit f une fonction définie sur un intervalle I.
L’intégration est l’opération inverse de la dérivation.
Calculer une intégrale de la fonction f(x) revient à calculer l’aire sous la courbe représentative
de f ou à calculer une primitive de f (x).
On appelle primitive de f toute fonction F dérivable sur I et telle que F ’ = f.
f(x)dx =F(x)
[ ]
a
b=F(b)+k!(F(a)
a
b
"+k)=F(b)!F(a)
Quelques propriétés des intégrales
- Relation de Chasles :
Quelque soit l’ordre des réels a, b et c,
f(x)dx
a
c
!=f(x)dx +f(x)dx
b
c
!
a
b
!
- Linéarité
(1)
(f+g)(x)dx =f(x)dx +g(x)dx
a
b
!
a
b
!
a
b
!
(2)
! f(x)dx = ! f(x)dx
a
b
!
a
b
!
, avec λ un réel.
- Effet de la parité
Si f est paire sur
!a;a
[ ]
, alors
f(x)dx =2f(x)dx
0
a
!
"a
a
!
Si f est impaire sur
!a;a
[ ]
, alors
f(x)dx =0
!a
a
"
Primitives des fonctions usuelles
Fonction
Primitive (sans « + Cste »)
un
1
n+1
un+1
1
u
ln u
eau+b
1
a
eau+b
1
1+u2
arctan u

Les!Extr@s!du!C2P1! BIOMATHS! n°1!INTÉGRATION!
!
!
3!
sin u
!cosu
cosu
sin u
ln u
uln u!u
II) Procédés pour déterminer une intégrale
1) Méthode des rectangles (ou de la fonction en escalier)
Voici une méthode graphique permettant d’approcher la valeur de l’intégrale. Elle nous
permet de calculer une intégrale numérique (par opposition à intégrale analytique).
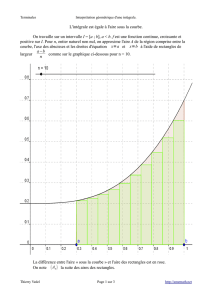
1. On décompose l’aire sous la courbe représentative de f en rectangles élémentaires de
largeur constante h (somme minorante ou majorante).
- dans le cas de rectangles « minorants » : aire entre x et x + h = h x f (x)
- dans le cas de rectangles « majorants » : aire entre x et x + h = h x f (x + h)
2. On somme les aires des rectangles élémentaires.
Un exemple : Soit
f(x)=!x2+5x
.
Représentation graphique de f (x)
Nous avons décomposé l’aire sous la courbe en rectangles minorants de largeur h = 0,5.

Les!Extr@s!du!C2P1! BIOMATHS! n°1!INTÉGRATION!
!
!
4!
Calculons l’intégrale suivante :
f(x)dx
0
2
!
f(x)dx
0
2
!=A(xi)
i=0
1,5
"
= Aire des rectangles n°1 (entre 0 et 0,5) + n°2 (entre 0,5 et 1) + n°3
(entre 1 et 1,5) + n°4 (entre 1,5 et 2)
f(x)dx
0
2
!=h"f(0) +f(0, 5) +f(1) +f(1, 5)
[ ]
=0, 5"0+2, 25 +4+5, 25
[ ]
=5, 75
ATTENTION : Il ne faut pas inclure f (2) dans le calcul ! Nous avons besoin de l’aire de 4
rectangles seulement. Pour 5 valeurs, il y a 4 intervalles. Reportez-vous au graphe, ce sera
plus clair.
2) Méthode des trapèzes
Encore une nouvelle méthode graphique pour calculer une approximation numérique de
l’intégrale.
Cependant elle utilise une approximation affine, car on approxime par segment de droite la
fonction. Elle est donc plus précise que la méthode des rectangles.
1. On décompose l’aire sous la courbe représentative de f en trapèzes élémentaires de hauteur
constante h.
RAPPEL : Aire d’un trapèze =
petite base +grande base
2!h
Dans le cas de nos trapèzes élémentaires :
Aire entre x et x +h=f(x)+f(x+h)
2!h
2. Enfin on somme toutes ses aires élémentaires :
Intégrale = Somme des trapèzes =
f(a)
2+f(x1)+... +f(xn)+f(b) 2
!
"
#$
%
&'h
Un exemple : Soit
g(x)=!x2+5x+2
g(0) = 2
g(1) = 6
g(2) = 8
g(3) = 8
g(4) = 6
g(5) = 2

Les!Extr@s!du!C2P1! BIOMATHS! n°1!INTÉGRATION!
!
!
5!
Représentation graphique de g
Nous avons décomposé l’aire sous la courbe représentative de g en trapèzes de hauteur h = 1.
Calculons par la méthode des trapèzes l’intégrale :
g(x)dx
0
5
!
g(x)dx
0
5
!=g(0)
2+g(1) +g(2) +g(3) +g(4) +g(5) 2
"
#
$%
&
'(h
=2
2+6+8+8+6+2 2
"
#
$%
&
'(1
=30
Méthode des trapèzes et concavité
Fonction concave (concavité vers le bas)
Fonction convexe (concavité vers le haut)
L’intégrale numérique calculée par la
méthode des trapèzes est inférieure à
l’intégrale analytique
L’intégrale numérique calculée par la
méthode des trapèzes est supérieure à
l’intégrale analytique