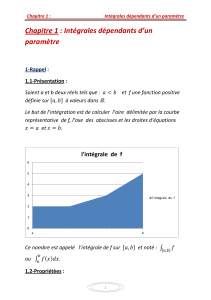
Chapitre 1 : Intégrales dépendants d’un paramètre Chapitre 1 : Intégrales dépendants d’un paramètre 1-Rappel : 1.1-Présentation : Soient a et b deux réels tels que : < définie sur , à valeurs dans ℝ. et f une fonction positive Le but de l’intégration est de calculer l’aire délimitée par la courbe représentative de f, l’axe des abscisses et les droites d’équations = et = . l'intégrale de f 6 5 4 3 l'intégrale de f 2 1 0 a b Ce nombre est appelé l’intégrale de f sur ou . 1.2-Propriétèes : 1 , et noté : , Chapitre 1 : Intégrales dépendants d’un paramètre , Soient f et g deux fonctions continues par morceaux sur 1- L’intégrale est une forme linéaire sur l’espace vectoriel des fonctions continues par morceaux sur , . 2- Relation de Chasles : ∀ , : = + . Ainsi, l’intégrale d’une fonction continue par morceaux est la somme d’intégrales de fonctions continues. , 3- Si f est positive sur 4- Si ≤ sur , alors , 5- Si f est continue par morceaux sur par morceaux sur , et : 6- Inégalité de la moyenne : ≤ ≤ En particulier, ≥ 0. alors !| !| ≤ |, alors | | continue | ≤ , |, . , " " | | . | − . 7- Inégalité de Cauchy-Schwartz : $ & % ≤$ & %$ & %. Cette inégalité s’écrit aussi : ≤$ & 8- Somme de Riemann : 2 ' ( % $ & ' ( %. . Chapitre 1 : Intégrales dépendants d’un paramètre - 2:8 ) f x dx = lim 6 x748 − x7 f C7 . x< , x8 , … , x2 où 2→45 7;< est une subdivision de a, b et C7 ϵ x7 , x748 . 1.3- Différentes méthode de calculs : 1.3.1- Théorème fondamentale de l’intégration : Théorème : Soit : A → ℝ une fonction continue et x< A. ↦ La fonction : . D DE C C est dérivable et F FD $ D DE C C% = En conséquence, toute fonction réelle continue sur un intervalle I y admet des primitives. Remarques : 1- Si f est une fonction continue de I dans ℝ et F est une de ses primitives alors : ∀ , A& : ) C C= G C 2- Si f est de classe H 8 , alors : Exemples : 123- 8 J C < C=K 8 FL < 84L ( V ( < U & L MN' 8 O = J48 < = PQ C RC C C= 8 J48 8 < V 84 ( < −G D = ′ C . = . S T WX &L & − =G C=K + L & 3 V XYJ &L ( O T < = . S T C. Chapitre 1 : Intégrales dépendants d’un paramètre 1.3.2- Intégration par parties : Soient f et g deux fonctions de classe H 8 sur un intervalle I et , A& . On a: ′ C Exemples : C 1- Calculons : A = ] Posons : \ Par suite, A= − & C= S < & = [R = &+2 +2 U C C +2 − [R . \ alors S < + S < ′ C C. =− U . =2 +2 ′ 2 +2 U S = ^ + 2^ + 2 ) & C +1 U < Une deuxième intégration par parties nous donne : A =^ ^+2 +2 2- Calculons : a = Posons : \ = ] Par suite : a = K$ Df T + & + 1 [R d 8 b +2 = cR b d % cR O − 8 S < − + 2 cR d Dg $ 8 T S < [R . alors e + % = 4 = ^ ^ + 2 − 4. ′ df T = Df T + = 8 D +h −K & & Df 8i + D( O d & 8 Chapitre 1 : Intégrales dépendants d’un paramètre = 3 T 1 & 9 h + h + 16 2 16 1.3. 3- Calcul par changement de variables : Proposition : Soient I et J deux intervalles de ℝ, : A → ℝ une fonction continue et m: a → A une fonction de classe H 8 . Si , a& alors : n n C C= om pm′ . Exemples : 1- Calculons l’intégrale suivante : A = Posons C = h D . On a donc : Par suite : A= d L 8 √L48 2- Calculons : C= d L48 8 √L48 ⇒ = FL L . C d 2 b = t √C + 1 − 2√C + 1u 3 8 a= a= d 8 8 √L48 C− &d √vJD d D Posons : C = cR . On a donc : Par suite : C = hD 8 d (q < √d q 48 84vJ& √C 8 . C= FD D b 84vJ& C = K √C O b & 8 . 2- Interversion limite- intégrale et sommation- intégrale : 2.1- limite- intégrale : 5 Chapitre 1 : Intégrales dépendants d’un paramètre 2.1.1- Théorème de convergence monotone : Soit J J une suite de fonctions positives continues par morceaux sur un intervalle I. On suppose que : note sa limite. ∀ A: o J pJ est une suite croissante, on La fonction f est alors continue par morceaux sur I et la suite $ w % J J croît vers w . 2.1.2- Lemme de Fatou : Soit J J une suite de fonctions positives continues par morceaux sur I. La fonction lim [R l’on a : J ) lim [R w est alors continue par morceaux sur I et J ≤ lim [R ) w J 2.1.3- Théorème de convergence dominée : Soit si : J J une suite de fonctions continues par morceaux sur I 1- La suite J J converge simplement vers une fonction f continue par morceaux sur I. 2- Il existe une fonction : A → ℝ4 continue par morceaux et intégrable sur I vérifiant la condition de domination suivante : ∀ A ∀R ℕ: | J | ≤ . Alors, les fonctions J et f sont intégrables sur I et : 6 Chapitre 1 : Intégrales dépendants d’un paramètre lim ) =) J J→45 w w Exemples : 1- Etudions lim y z 84&XYJ$M% limJ→45 :z 84L ( Posons : ∀R ℕ : ∗ J C = y 84&XYJ$ % M 84L ( J w C. On a bien : ∀C −|, | ∀R ℕ∗ : | intégrable sur −|, | . De plus, la suite o =) J J→45 C = et J C |≤ b 84L ( . C avec g est C pJ converge simplement vers Donc d’après le théorème de convergence dominée, 8 84L ( . C z 1 + 2 [R $ % 1 R lim ) C = ) C = 2PQ C R| & J→45 :z 1 + C& 1 + C :z z 2- Calculons : limJ→45 45 :L M h < C. 2.2- Interversion sommation- intégrale : 2.2.1- Théorème d’intégration terme à terme : Soit J J une suite de fonctions continues par morceaux et intégrables sur I, si : 1- La série de fonctions ∑ J converge simplement vers une 45 fonction = ∑J;< J qui est continue par morceaux sur I. 2- La série numérique ∑ w | J | converge. Alors, la fonction g est intégrable sur I et 7 Chapitre 1 : Intégrales dépendants d’un paramètre 45 ) = 6) w Autrement dit, 45 ) 6 w Exemple : On sait que : Donc, J;< 45 = 6) J C = ∑45 J;< 8 J( : . 45 J ∀C 0,1 : ∑J;< C = 45 ∀C 0,1 : ∑J;< −cRC C J = Par suite : 8 45 ∑ < J;< J J;< w 8 vJL < L:8 Montrons que : J J;< w 8:L vJL . L:8 −cRC C J C = Posons : ∀C 0,1 , ∀R ℕ: 8 8 vJL < L:8 C. C = −cRC C J . J 1- Ces fonctions sont continues et intégrables sur 0,1 , en effet : limL→< √C zéro. J C = 0 . Donc De plus, limL→8 J vJL L:8 J converge simplement vers la fonction qui est continue sur 0,1 . 3- La série numérique ∑ 8 ) | < J C est intégrable au voisinage de C = 0. D’où le résultat. 2- La série fonctions ∑ C = J 8 8 | < J C | C converge, en effet : C | C = ) | −cRC C < 8 J| 8 C = ) −cRC C J C < Chapitre 1 : Intégrales dépendants d’un paramètre Par une intégration par parties on trouve : 8 | < J C | C= 8 J48 ( . d’où la série converge. Donc, en utilisant le théorème d’intégration terme à terme, on obtient : 45 cRC 1 ) C=6 R+1 < C−1 8 J;< 45 =6 & J;8 3-Intégrale dépendant d’un paramètre: • € ƒ 3.1- La fonction : ~ • = 3.1.1- Proposition : 1 R& • ‚•: A. Soient f une fonction continue par morceaux sur I et G La fonction : = 3.1.2- Théorème : D C C est continue sur I. Si f est continue sur I alors la fonction : est une primitive de f sur I . G = D C C C’est l’unique primitive de f qui s’annule en a. 3.1.3- Remarques : 1. Si f est continue sur I et „ = D C A alors la fonction : C est dérivable sur I et „′ 2. Si f est continue et positive sur ) =0 ⇔ 3.1.4- Proposition : 9 , ≡0 =− alors : Q , . Chapitre 1 : Intégrales dépendants d’un paramètre Soient f une fonction continue sur I , ‡ et ˆ deux fonctions dérivables sur un intervalle J à valeurs dans I. La fonction définie sur J par : m dérivable sur J et : m′ 3.1.5- Exemples : = ˆ′ oˆ = ‰ D Š D p − ‡′ C o‡ C est p 1. Soit f une fonction continue sur ℝ. La fonction : G = &D D C est dérivable sur ℝ et : C ∀ ℝ: G′ 2. Considérons „ =2 2 dq PQ D( = [R C − . C tel que −1,0 . La fonction C = PQ [R C est continue sur A = −1,1 , les deux fonctions ‡ = & et ˆ = h D sont dérivables sur a = −1,0 à valeurs dans I . Donc, G est dérivable sur −1,0 et ∀ −1,0 : „′ = h D PQ [R h D − 2 PQ [R & 3.2- Fonctions définies par des intégrales : Soient I un intervalle et f une fonction numérique définie sur , × A. Théorème 1 : Si f est continue sur ∀Œ A, la fonction : la fonction : G Œ = Théorème 2 : •: , × A alors : ↦ ,Œ , Œ est intégrable sur est continue sur I. 10 , et Chapitre 1 : Intégrales dépendants d’un paramètre Si de plus, la fonction f admet une dérivée partielle continue sur , × A alors : Ž• Ž• qui est F est continûment dérivable sur I et ∀Œ A: G′ Œ = ) • •Œ ,Œ Autrement dit, pour dériver F, on peut dériver sous le signe de l’intégrale. Théorème 3 : Si f et Ž• Ž• sont continues sur de classe H 8 de A → „ Œ = ‘ • ’ • ‘ • „′ Œ = ) ’ • Exemple : ,Œ • •Œ , , × A et u et v deux fonctions alors, la fonction G définie par : est dérivable sur I et : ,Œ + “ Œ , Œ “′ Œ − Etudier la dérivabilité de : „ Œ = Œ ,Œ ′ Œ d ” D WX• h • 3.3- Applications à des calculs d’intégrales : La dérivation sous le signe de l’intégrale permet de calculer certaines intégrales plus rapidement surtout lorsqu’on ne connait pas de primitive. Exemple : Soit C > 0 , calculons l’intégrale : G C = Posons : „ C = 8 8 < D ( 4L ( et 11 8 8 ( < D 4L ( ( m ,C = 8 D ( 4L ( . . Chapitre 1 : Intégrales dépendants d’un paramètre ∈ 0,1 , m est dérivable par rapport Il est claire que pour tout à t sur ℝ4∗ et : Žn ŽL ,C = − 0,1 × ℝ4∗ . &L D ( 4L ( ( et cette dérivée est continue sur Donc d’après le théorème précèdent, G est continument dérivable sur ℝ4∗ et sa dérivée : „ ] C = −2CG C D’une autre part, „ C = Par suite, „] C = − =− D’où : G C =− Finalement, 8 ) < 1 1 PQ C R — ˜ C C 1 1 1 1 PQ C R — ˜ − ™ š C& C Cb 1 + 1 C& 1 1 1 1 PQ C R — ˜ − — ˜ C& C C 1 + C& 1 1 1 ] 1 1 „ C = & — PQ C R — ˜ + ˜ 2C C 1 + C& 2C C 1 & + C& & = 1 1 1 1 — PQ C R — ˜ + ˜ 2C & C C 1 + C& 3.4- Fonctions définies par une intégrale généralisée : Soient I un intervalle et f une fonction de deux variables continue sur , +∞ × A. 12 Chapitre 1 : Intégrales dépendants d’un paramètre On considère la fonction F définie sur I par : G Œ = 45 ,Œ 3.4.1- Théorème1 : S’il existe une fonction positive g définie, continue par morceaux et intégrable sur , +∞ telle que : ∀ ,Œ ∈ , +∞ × A: | ,Œ | ≤ Alors, F existe et continue sur I. 3.4.2- Théorème2 : Si de plus f admet une dérivée partielle Ž• Ž• continue sur , +∞ × A et il existe une fonction positive h définie, continue par morceaux et intégrable sur , +∞ telle que : ∀ ,Œ ∈ , +∞ × A: œ Alors, F est de classe H 8 sur I et : G′ Œ = 45 Ž• Exemple : Calculons : Posons : Ž• • •Œ ,Œ œ ≤ ℎ ,Œ A Œ = 45 :D ( h < , Œ = h :D U ( U Œ Œ tel que : pour Œ ∈ ℝ. , Œ ∈ 0, +∞ × ℝ. La fonction f est continue sur 0, +∞ × ℝ et : | ,Œ | ≤ = h :D , ( avec g est positive continue et intégrable sur 0, +∞ . Donc, la fonction I est bien définie et continue sur ℝ. 13 Chapitre 1 : Intégrales dépendants d’un paramètre De plus, f est dérivable par rapport à y de dérivée partielle : • •Œ , Œ = − h :D [R Œ ( Ž• Ž• Il est clair que la fonction œ • •Œ est continue sur 0, +∞ × ℝ et : ,Œ œ ≤ ℎ = h :D ( avec h est positive continue et intégrable sur 0, +∞ . Alors, I est de classe H 8 sur ℝ et : 45 A Œ =) ] < • •Œ = −) ,Œ En intégrant par parties, on trouve : 45 < h :D [R Œ ( 45 45 1 Œ ( ( A] Œ = t h :D [R Œ u − ) h :D U 2 2 < < Par suite, wž • w • =− Œ =− A Œ 2 • & D’où, en intégrant par rapport à y, on a : Or, A 0 = A Œ = 45 :D ( h < •( :T Hh = √^ = H & 8 Finalement, A Œ =) 45 < h :D ( U Œ 14 •( 1 :T = √^h 2 Œ
