Cours-de-1S-maths-1

COURS ET EXERCICES DE MATHEMATIQUE FKM 2014 Page 1
Rédigé par :
 !"#$% &'(()*+,-./ &'((0(12-32
456%+!7!#8,39 4:/9 )*-;''4:/9
Dakar, Septembre 2013

COURS ET EXERCICES DE MATHEMATIQUE FKM 2014 Page 2
Ce livre s’adresse aux élèves des classes de Première S. Conforme aux Programmes
officiels en vigueur dans les séries S1, S2 et S3, il a pour but de leur présenter les
connaissances indispensables et de mettre à leur disposition de nombreux exercices et
problèmes pour appliquer celles-ci. Il n’est cependant pas un substitut au Cours du
Professeur qui demeure irremplaçable.
Chaque notion du cours introduite a été illustrée d’exemples et tous les résultats du
programme sont démontrés. Nous avons évité cependant toute digression inutile, nous
concentrant sur l’essentiel. Nous avons voulu être très pratiques et ne donner à l’élève que
ce dont il a vraiment besoin pour réussir les évaluations et avoir le niveau requis pour
affronter la classe suivante (Terminale S1 ou S2). Tout discours superflu (par exemple sur
l’histoire ou la biographie des mathématiciens) a donc été omis.
En général, un élève ne pourra pas étudier toutes les situations présentées dans ce
livre, mais, sous la guidée de son Professeur, il pourra sélectionner les notions et exercices
qui correspondent à des objectifs précis, en fonction de sa classe et de sa série.
Il ne s’agit pas d’un traité aux prétentions encyclopédiques mais, plus modestement,
d’un outil de travail qui veut éviter à l’élève, comme c’est le cas actuellement, de devoir
consulter une demi-douzaine d’ouvrages pour bien maîtriser les concepts.
Nous espérons que cet humble travail, malgré ses imperfections, sera utile aux
élèves et aux collègues. Nous remercions par avance toute personne qui voudra bien nous
faire part de remarques ou suggestions pour l’améliorer.
LES AUTEURS

COURS ET EXERCICES DE MATHEMATIQUE FKM 2014 Page 3
TABLE DES MATIERES
CHAPITRE 1 : DENOMBREMENT (Page 5)
CHAPITRE 2 : EQUATIONS, INEQUATIONS ET SYSTEMES (Page 43)
CHAPITRE 3 : GENERALITES SUR LES FONCTIONS (Page 79)
CHAPITRE 4 : FONCTIONS POLYNÔMES (Page 120)
CHAPITRE 5 : VECTEURS, REPERES, BARYCENTRES (PAGE 147)
CHAPITRE 6 : GEOMETRIE DANS L’ESPACE (Page 177)
CHAPITRE 7 : PRODUIT SCALAIRE DANS LE PLAN (Page 226)
CHAPITRE 8 : ANGLES ORIENTES ET TRIGONOMETRIE (Page 263)
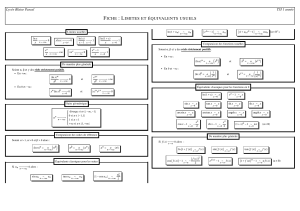
CHAPITRE 9 : LIMITES ET CONTINUITE (Page 327)
CHAPITRE 10 : DERIVEES ET APPLICATIONS (Page 351)
CHAPITRE 11 : ETUDE DE FONCTIONS (Page 368)
CHAPITRE 12 : PRIMITIVES (Page 396)
CHAPITRE 13 : SUITES NUMERIQUES (Page 400)
CHAPITRE 14 : STATISTIQUES (Page 432)
CHAPITRE 15 : TRANSFORMATIONS DU PLAN (Page 461)
CHAPITRE 16 : ORTHOGONALITE ET PRODUIT SCALAIRE DANS L’ESPACE (Page 507)

COURS ET EXERCICES DE MATHEMATIQUE FKM 2014 Page 4

COURS ET EXERCICES DE MATHEMATIQUE FKM 2014 Page 5
CHAPITRE 1 : DENOMBREMENT
1. INTRODUCTION
L’objet du dénombrement est, comme son nom l’indique, de compter le nombre
d’éléments d’un ensemble bien défini c’est-à-dire d’un ensemble dont les éléments
possèdent une propriété ne posant aucun problème d‘ambiguïté.
Compter peut s’avérer assez délicat dans des cas complexes où l’on ne « voit pas » les
objets qu’on souhaite dénombrer. Voici par exemple des exercices simples de
dénombrement :
• Combien de mots de quatre lettres distinctes ou non peut-on constituer avec l’al-
phabet?
• Dix athlètes prennent le départ d’une course. Combien y a-t-il d’arrivées possibles ?
• Combien y a-t-il de façons de sélectionner une équipe de 6 joueurs parmi les 10
membres d’un club?
Nous allons mettre en place des outils et méthodes pour résoudre ce type de problèmes.
Le dénombrement utilise un vocabulaire spécialisé tel que : combinaison, 8-liste,
arrangement, permutation, ensemble, cardinal d’un ensemble, réunion, intersection,
complémentaire, …
Les outils utilisés en dénombrement sont très variés : des entiers naturels particuliers
tels que 2<,"
=
>
,+
=
>
et 2
>
, des représentations telles que le diagramme de Venn, les
diagrammes sagittaux , les arbres de choix , les tableaux à double entrée …
Les problèmes de dénombrement se ramènent aussi parfois à des situations où on doit
déterminer le nombre de façons d’obtenir p éléments choisis parmi 2 éléments donnés.
Devant de telles situations, les questions qu’on se pose sont :
-Les éléments sont-ils choisis sans ordre ou avec ordre ?