analyse fourier

Cours d’analyse de Fourier
avec exercices
niveau L3 physique
Eric Aristidi
Version du 4 novembre 2020

Table des mati`eres
1 Signaux discontinus — Distribution de Dirac 3
1.1 LafonctiondeHeaviside........................................... 3
1.2 Lafonctionporte............................................... 4
1.3 DistributiondeDirac............................................. 5
1.3.1 Approcheheuristique ........................................ 5
1.3.2 Propri´et´e fondamentale — D´efinition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3.3 Quelquespropri´et´es ......................................... 7
1.3.4 D´eriv´ees de signaux discontinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.4 PeignedeDirac................................................ 11
1.5 Distribution de Dirac bidimensionnelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2 La convolution 13
2.1 D´efinition ................................................... 13
2.1.1 D´efinition............................................... 13
2.1.2 Significationphysique ........................................ 13
2.2 Propri´et´esdelaconvolution......................................... 13
2.2.1 La convolution est un produit commutatif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2.2 Autrespropri´et´es........................................... 15
2.3 Application `a la r´esolution d’´equations diff´erentielles lin´eaires . . . . . . . . . . . . . . . . . . . . . . 17
2.3.1 Exemple................................................ 17
2.3.2 G´en´eralisation ............................................ 18
2.3.3 Calcul de la r´eponse impulsionnelle : exemple du ressort . . . . . . . . . . . . . . . . . . . . . 19
3 Transformation de Fourier 21
3.1 D´efinition ................................................... 21
3.1.1 D´efinition............................................... 21
3.1.2 Transform´ee de Fourier des fonctions `a valeurs r´eelles . . . . . . . . . . . . . . . . . . . . . . 21
3.1.3 Exemples ............................................... 22
3.2 Propri´et´esdelaTF.............................................. 24
3.2.1 Lin´earit´e ............................................... 24
3.2.2 Changement de signe et conjugaison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.2.3 Valeur`al’origine........................................... 25
3.2.4 Changementd’´echelle ........................................ 25
3.2.5 Translation .............................................. 25
3.2.6 Multiplication par un terme de phase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.2.7 Tranform´ee de Fourier inverse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.2.8 Signification physique de la TF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.2.9 D´erivation............................................... 29
3.2.10 TF d’une convolution et d’un produit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2.11 TFd’unefonctioncausale...................................... 33
3.2.12 CommentcalculeruneTF...................................... 34
3.3 Fonctions de transfert et filtrage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.3.1 Exemple : circuit RC ........................................ 35
3.3.2 Quelquesd´efinitions ......................................... 37
3.4 Corr´elations et spectres de puissance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.4.1 Fonctionsdecorr´elation....................................... 40
3.4.2 Spectresdepuissance ........................................ 43
2

TABLE DES MATI` ERES 3
3.4.3 Th´eor`emes de Wiener-Kinchin et Parseval . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.4.4 Relationsd’incertitude........................................ 44
4 S´eries de Fourier — Echantillonnage 45
4.1 S´eriesdeFourier ............................................... 45
4.1.1 TFdupeignedeDirac........................................ 45
4.1.2 Formule sommatoire de Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.1.3 S´eriedeFourier............................................ 48
4.1.4 Exemples ............................................... 50
4.2 Echantillonnage................................................ 52
4.2.1 D´efinition............................................... 52
4.2.2 Transform´ee de Fourier d’une fonction ´echantillonn´ee . . . . . . . . . . . . . . . . . . . . . . . 53
4.2.3 Th´eor`eme de Shannon-Nyquist . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
4.2.4 D´es´echantillonnage — Interpolation de Shannon . . . . . . . . . . . . . . . . . . . . . . . . . 56
5 Exercices 60
5.1 Impulsion δdeDirac............................................. 60
5.1.1 Fonctions usuelles en analyse du signal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
5.1.2 Translation et dilatation d’un signal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
5.1.3 ImpulsiondeltadeDirac....................................... 61
5.1.4 D´eriv´ees de signaux discontinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
5.1.5 PeignedeDirac............................................ 61
5.1.6 D´eriv´ee de la distribution δ..................................... 62
5.2 Filtrelin´eaireetconvolution......................................... 63
5.2.1 Produitdeconvolution........................................ 63
5.2.2 R´eponsesimpulsionnelles ...................................... 63
5.2.3 Distributiondephotons ....................................... 64
5.3 Transform´eedeFourier............................................ 64
5.3.1 Calculs de transform´ee de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
5.3.2 Op´erationssurlessignaux...................................... 65
5.3.3 Contrastedephase.......................................... 65
5.3.4 D´econvolution ............................................ 66
5.3.5 TFoptique .............................................. 66
5.3.6 Enregistrementd’unson....................................... 66
5.3.7 Filtreslin´eaires............................................ 67
5.3.8 Filtrageoptique ........................................... 68
5.4 Corr´elation et spectre de puissance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
5.5 S´eriesdeFourier ............................................... 69
5.6 Echantillonnage et p´eriodisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
5.6.1 Acc´el´eration de convergence d’une s´erie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
5.6.2 Echantillonnage d’un signal `a bande ´etroite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.6.3 Lien entre la formule de Shannon et la s´erie de Fourier . . . . . . . . . . . . . . . . . . . . . . 71
Annexe : Formulaire de Transform´ees de Fourier 73

Chapitre 1
Signaux discontinus — Distribution de
Dirac
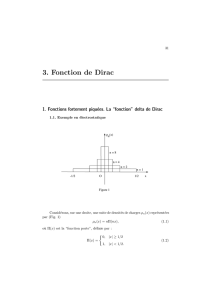
1.1 La fonction de Heaviside H(x)
H(x) est une fonction d´efinie de R∗vers l’intervalle [0,1] et qui vaut :
H(x) = 0 si x < 0
H(x) = 1 si x > 0(1.1)
1,25
0,75
0,25
H(x)
1,0
0,5
0,0
x
1050
On parle parfois de fonction ´echelon ou d’´echelon unit´e (“unit step” en anglais). H(x) n’est pas d´efinie en 0 1.
Cependant, on fera parfois un prolongement par continuit´e lorsque cel ? s’imposera ; par exemple la fonction H(x)+
H(−x) vaut 1 ∀x6= 0 mais n’est pas d´efinie en 0. On la prolongera donc (en lui donnant la valeur 1) en x= 0 de
mani`ere `a ce qu’elle soit continue sur R.
On d´efinit parfois H(x) en utilisant une fonction quelconque f(d´efinie de Rvers R) dite fonction test par l’´egalit´e
Z∞
−∞
f(x)H(x)dx =Z∞
0
f(x)dx (1.2)
c’est la d´efinition au sens des distributions (la th´eorie des distributions ne sera cependant pas abord´ee dans ce
cours).
En physique, H(t) est parfois utilis´ee pour les fonctions du temps tqui sont nulles `a t < 0. Par exemple, un caillou
lˆach´e `a t= 0 depuis l’altitude z0sans vitesse initiale a un mouvement d´ecrit par l’altitude z(t) = z0−1
2gt2H(t).
Un autre exemple en optique est le coefficient de transmission d’un demi-plan.
1. Il existe d’autres d´eterminations `a l’origine selon les auteurs. On pourra ainsi trouver H(0) = 0, H(0) = 1 ou H(0) = 1
2.
4

CHAPITRE 1. SIGNAUX DISCONTINUS — DISTRIBUTION DE DIRAC 5
H(sin(x))
x
105
0,25
0−5
1,0
0,75
0,0
0,5
−10
4
0,75
0
x
6
H(3x+2)
1,0
0,5
2
0,25
0,0
−2
−5
0,75
x
0
H(−x)
1,0
0,5
−10
0,25
0,0
π 2π
H(sin(x))H(3x+2)H(−x)
−2/3
Figure 1.1 – Exemples de fonctions de Heaviside
1.2 La fonction porte Π(x)
La porte Π(x) est aussi une fonction discontinue d´efinie par morceaux :
Π(x) = 1 si |x|<1
2
Π(x) = 0 sinon (1.3)
−0,5 0,5
0,25
x
1,0
1,0
0,75
0,5
0,0
0,0−1,0
Elle n’est pas d´efinie sur les deux bords x=±1
2(mais on pourra appliquer des prolongements pas continuit´e si
n´ecessaire). On dit que cette fonction est de largeur 1 ou de support 1, c’est `a dire qu’elle est non nulle sur un
intervalle de largeur 1. Π(x) est reli´ee `a la fonction de Heaviside par
Π(x) = H(x+1
2)−H(x−1 2) (1.4)
En physique on utilise parfois la fonction porte pour d´efinir des signaux de dur´ee finie. Ainsi la fonction
f(t) = Π t−b
a(1.5)
0 2
0,25
x
1,0
3
0,75
0,5
0,0
1−1
correspond `a une porte de largeur a(ou de dur´ee asi test un temps) centr´ee sur la valeur t=b. Un autre exemple
est la densit´e de charge d’une boule de diam`etre Dcentr´ee sur l’origine de densit´e de charge uniforme ρ0. Sa densit´e
de charge dans tout l’espace s’´ecrit, en coordonn´ees sph´eriques (rd´esigne la distance `a l’origine) ρ(r) = ρ0Π( r
D).