TDquadripoles

VSVe
R R
R R
1 2
3 4 VsVe
i′i
R1
R2 3 R4 R
i i’
⃝
i
r
⃝
i
r
e
⃝
i e
⃝
ir
e
⃝
i
e
⃝
i1 i2
r
⃝
r
i2i1
r
⃝
e2
e1
r2
r1
⃝
Z
Z
Z
A
C
B
⃝
Z
⃝
R1
R3R4
V V
1 2
i1i2
R2
R1= 1kΩ R2= 2kΩ R3= 3kΩ R4= 4kΩ
⃝
R1
V1
i1i2
V2
R2
1
.iα
⃝
R1
V1
i1R2
V2
i2
δ.V
1
.iα2

i1i2
R2
V1V2
R3
R1
a.V2
R1
V1
i1
R2
i2
V2
1
Y.V R3
R1= 1kΩ R2= 10kΩ R3= 100kΩ y= 0.05S
RL 1
1
v
i
ZC
RA
Zev
ZeRL
ZC
Ze=Z0=RL
RA=RB=RL= 1kΩ
α β δ
R1Z1Z2R2
R α β Y
1
R1
Y1Y2
1
R2
100Ω 0 15 10S

Y ij
V1
i1i2
V2
11
Y + Y
21
Y + Y
2122
−Y
21
12 21
(Y −Y )V2
R1= 1kΩ R2= 1Ω RL= 100Ω β= 1500 Ω V1= 10V
dBm
⃝
V2
i2 i1
R1
V1RL
⃝
R2
V2
i2
R1V1
i1
RL
1
β.i
RL
eg
g
R
R2
i2
V2
ia
V1
i1
RbRa
.iαa
e
Rg
RaRbR2α eg
V1 V2
i2
R2i 1
R1iβ
i
RL
Rg
eg
e
Rg

Za
Zc
Za
Zc
Zc
ZbZa
R1
C R2
ω
R R
C
R
V1V2
i1i2
1 1
2
Y′Y′′
Y
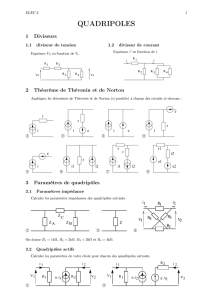
Vs=R3·R4
(R1+R2)(R3+R4) + R3·R4
Vei′=R2(R3+R4)
R2(R3+R4)+(R3·R4)i
Z Eth In⃝ ∞ − i⃝r e +ri i +e/r ⃝0e− ⃝ r e +ri i +e/r ⃝ ∞ − i⃝r r(i1+i2)
i1+i2⃝ ∞ − i1−i2⃝r1r2/(r1+r2) (r2e1+r1e2)/(r1+r2)e1/r1+e2/r2
⃝Z11 =ZA(ZC+ZB)/(ZA+ZB+ZC)Z12 =ZAZB/(ZA+ZB+ZC)Z22 =ZB(ZC+ZA)/(ZA+
ZB+ZC)⃝Zij =Z⃝Z11 = 2,4kΩ Z12 = 1kΩ Z22 = 2,5kΩ
⃝Z11 =R1Z12 = 0 Z21 =αR2Z22 =R2Y11 = 1/R1Y12 = 0 Y21 =−α/R1Y22 = 1/R2
h11 =R1h12 = 0 h21 =−α h22 = 1/R2⃝Z11 =R1Z12 =αR1Z21 =δR1Z22 =R2+αδR1
Y11 = 1/R1+(αδ)/R2Y12 =−α/R2Y21 =−δ/R2Y22 = 1/R2g11 = 1/R1g12 =−α g21 =δ g22 =R2
h11 =R1R2/(R1+R2)h12 = (R1+aR2)/(R1+R2)h21 =−R1/(R1+R2)h22 = (R1+R2+
R3(1 −a))/((R1+R2)R3)
Y11 = 1,1mS Y12 =−0,1mS Y21 = 0,0499S Y22 = 0,11mS Z11 = 21,52Ω Z12 = 19,56Ω
Z21 =−9763Ω Z22 = 215Ω
Zev=ZCZe= (ZC(RA+RL))/(ZC+RA+RL)ZC= (Z2
0+Z0RA)/RA= 2kΩ
⃝ZE=R1+RLAV=RL/(R1+RL)Ai=−1ZS=R1GV=−20,8dB 9,17dBm
⃝β=Z ZE=R1AV=−ZRL/R1(R2+RL)Ai=Z/(R2+RL)ZS=R2GV= 3,44dB 33,4dBm
ZE= (RaRb)/(Ra+Rb)AV=αR2/RaAVch =αR2RL/Ra(R2+RL)
Ai=−αR2Rb/(R2+RL)(Ra+Rb)AVg=αR2Rb/(Rg(Ra+Rb) + RaRbZS=R2
ZS= ((Rg+R1)R2+RgR1)/(1 + β)(Rg+R1)
⃝1ZA01 101/ZC1
⃝1 + ZA/ZCZA1/ZC1 (ZC+ZA)/ZC(ZAZB+ZCZB+ZAZC)/ZC1/ZC(ZB+ZC)/ZC
Y′
11 = 1/R2Y′ 21 =−1/R2Y′′ 11 = (1 + jR1Cω)/(2R1+jR2 1Cω)Y′′ 21 = (−1)/(2R1+jR2 1Cω)