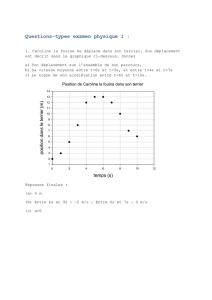
Exercices de mécanique : Analyse des contraintes câbles/poutres

Exercice 7A
La figure ci-contre montre un câble d’acier de 1 mm de diamètre constitué de 7
fils de 360
μ m de diamètre enroulés autour d’une poulie de 30 cm de diamètre
et supportant une charge de 70 N. Déterminer la contrainte normale de
tension maximale à laquelle ce câble est soumis. Préciser aussi quelle fibre sur
le câble subit cette contrainte.
(Rép. :
σ
max = (F/A) + (E y/r) = 98,2 MPa + 239,7 MPa = 337,9 MPa, sur la
fibre à la surface du fil qui touche à la poulie là où celui-ci la contourne.)
Données :
Matériau du câble = acier
⇒ E = 200×109 Pa
Df = diamètre d’un fil = 360
μ m =360×10–6 m
Dp = diamètre de la poulie = 30 cm = 0,30 m
F = force supportée par le câble = 70 N
La contrainte normale σ est maximale lorsque la contrainte σ
F
due à la force de traction de 70 N s’ajoute à la contrainte σ
flexion
due à courbure du câble autour de la poulie.
Calcul de σ
F = F / An
A
n = section de 7 fils ayant chacun un diamètre de 360×10–6 m
= 7× π ×(360×10–6)2 ÷ 4 = 712,513×10–9 m2.
σ
F = F / An = 70 ÷ 712,513×10–9 = 98,244×106 Pa
Calcul de la valeur maximale de σ
flexion.
Puisque
σ
flexion = Ey / r, elle atteint sa valeur maximale pour
y = ymax = le rayon d’un fil = 360×10–6 ÷ 2 = 180×10–6 m
et
r = rmin = rayon de la poulie + rayon d’un fil = 0,15m + 0,00018m = 0,150180 m
⇒ σ
flexion maximal = Eymax / rmin = 200×109 ×180×10–6 ÷ 0,150180 = 239,712×106 Pa
σ
max =
σ
F +
σ
flexion maximal = 98,244×106 + 239,712×106 = 337,96×106 Pa = 338 MPa
Ce sera sur la fibre ayant la plus petite valeur de « r » soit sur la fibre à la surface du fil qui
touche à la poulie là où celui-ci la contourne.
7
0 N
NOM : ……………………………………………………..
À compléter avant : ………………………………………………………………………………

203-001 D ch. 7 D7.2
Exercice 7B
Soit la poutre chargée ci-dessous laquelle est en bois de construction. Elle a une section droite rectangulaire pleine
de 20 cm
× 15 cm. Calculer les contraintes normale et de cisaillement maximales ainsi que son facteur de sécurité.
On néglige le poids propre de la poutre.
(Rép. : Vmax = 6,5 kN pour 6 < x < 8 ; Mmax = 8 kN.m à x = 6 m ; σ
max = 8,00 MPa;
τ
max = 0,325 MPa et F.S. = 6,9)
Solution :
La formule donnant la contrainte normale maximale est :
σ
max = Mmax / S
Le module de flexion « S » de la poutre doit être calculé avec la formule Sx = h2e /6
Avec h = dimension verticale = ………0,20 m…… et e = dimension horizontale = ……0,15 m……….
⇒ Sx = h2 b / 6 = 0,202×0,15 ÷ 6 = 1,0000 × 10 –3 m3
Pour obtenir la contrainte normale maximale pour toute la poutre, il suffit donc de calculer Mmax, la valeur du
moment fléchissant maximal pour toute la poutre.
La formule donnant la contrainte de cisaillement maximale est :
τ
max = 1,5 he
Vmax dans laquelle
V = effort tranchant maximal pour toute la poutre.
h = hauteur du profilé = ………0,20 ……. m et e = épaisseur du profilé = ……0,15………… m
Pour déterminer les contraintes normale et de cisaillement maximales pour toute la poutre, il suffit de calculer
respectivement « Mmax » et « Vmax », le moment fléchissant et l’effort tranchant maximaux pour toute la poutre. Pour
cela, il faut commencer par déterminer les réactions aux appuis « RG» et « RD». Nous devrons ensuite tracer le
diagramme de l’effort tranchant. Nous pourrons facilement y lire la valeur de Vmax. Pour obtenir la valeur de Mmax, il
faudra commencer par déterminer les endroits où V = 0 et y calculer la valeur de M. La valeur maximale obtenue
pour M est Mmax. Dans chaque cas on ne tiendra pas compte du signe.
1º Déterminons d’abord RG et RD, les réactions aux appuis :
Σ Mx=2 = – (3 kN/m×2 m)×1 m + RG×0 + 10kN×4m – RD×6m + 5kN×7m = 0
⇒ RD = (– 6 + 40 + 35) ÷ 6 = 11,5 kN
Σ Mx=8 = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = 0
⇒ RG = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = 9,500 kN
Vérification :
Σ Fy = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = 0 ⇒ OK!
0 5 8 9
h = 20 cm;
e = 15 cm
F2 = 5 kN
w = 3 kN/m
RG RD
F1 = 10 kN
6

203-001 D ch. 7 D7.3
2o On peut maintenant tracer le diagramme de l’effort tranchant
On peut lire sur le diagramme de V(x) que Vmax = 6 500 kN et se situe de x = 6 m à x = 8m
⇒ τ
max = 1,5 Vmax / he = 1,5× 6500 / (0,20×0,15) Pa = 0,325
× 106 Pa = 0,325 MPa
On peut lire sur le diagramme que Mmax est soit la valeur de M pour x = 2 m, soit la valeur de M pour x = 6 m , soit
la valeur de M pour x = 8 m, car ce sont les 3 seuls endroits, ailleurs qu’aux extrémités où V = 0.
On calcule donc M(x) pour chacune de ces 3 valeurs de x.
x
(m) Calcul de M(x) M(x)
(kN-m)
Méthode des équations méthode des surfaces sous V(x)
2 – 3×2×1 ou bien – 6×2÷ 2 – 6
6 – 3×2×(6 – 1) + 9,5×(6 – 2) ou bien – 6×2÷ 2 + 3,5×(6 – 2) + 8
8 – 3×2×(8 – 1) + 9,5×(8 – 2) –10×(8 –6) ou bien – 6×2÷ 2 + 3,5×(6 – 2) – 6,5×2 – 5
La valeur maximale du moment fléchissant est donc Mmax = 8,0 kN.m pour x = 6 m de l’extrémité gauche de la
poutre.
⇒ σ
max = Mmax / Sx = 8 000 ÷ 1,0000
× 10 –3 = 8,0000 × 10 6 Pa = 8 MPa
V (kN) Diagramme de l’effort tranchant
8
x (m)
0 1 57 8 10
2 3 4 6 9
6
4
2
0
-2
-4
-6
-8
0 8 9
h = 20 cm;
e = 15 cm
F2 = 5 kN
w = 3 kN/m
RG = 9,5 kN RD= 11,5 k
N
F1 = 10 kN
62
– 6
+ 3,5
– 6,5
+ 5
–6 kNm
+14 kNm
–13 kNm
+ 5 kNm

203-001 D ch. 7 D7.4
(d) Pour obtenir le facteur de sécurité global pour toute la poutre il suffit de le calculer à l’endroit où il est
minimale. Dans le cas d’un profilé en bois de construction, ça peut être aussi bien le facteur de sécurité relié à la
contrainte normale maximale pour toute la poutre que celui relié à la contrainte de cisaillement maximale pour toute
la poutre. Il faut prendre le plus petit des deux.
F.S. pour la contrainte normale =
σ
u /
σ
max avec
σ
u = 55 MPa (Tableau G en compression car plus faible)
F.S. pour la contrainte normale = σ
u /
σ
max = 55 MPa ÷ 8 MPa = 6,875
F.S. pour la contrainte de cisaillement = τ
u /
τ
max avec
τ
u = 3,5 MPa (Tableau G)
F.S. pour la contrainte de cisaillement = τ
u /
τ
max = 3,5 MPa ÷ 0,325 MPa = 10,77
⇒ Le F.S. global pour toute la poutre = 6,875 (On prend le plus petit des F.S.)
Exercice 7C
Soit la poutre chargée de la figure ci-dessous. Il s’agit du profilé d’acier en « H » W 310
× 45. Déterminer les
contraintes normale et de cisaillement maximales (a) pour x = 2 m; (b) pour x = 7 m; (c) pour toute la poutre.
(d) De plus, déterminer le facteur de sécurité global pour toute la poutre. On néglige le poids propre de la poutre.
1º Déterminons d’abord RG et RD, les réactions aux appuis :
Σ Mx=1 = 6 × 4 × (2 – 1) + 40 × (3 – 1) + 9 × 5 × (7,5 – 1) + 20 × (9 – 1) - (8 – 1) × RD = 0
⇒ RD = (24 + 80 +292,5 + 160) ÷ 7 = 79,5 kN
Σ Mx=8 =+(8 – 1) × RG - 6 × 4 × (8 – 2) - 40 × (8 - 3) - 9 × 5 × (8 – 7,5) + 20 × (9 – 8) = 0
⇒ RG = (144 + 200 + 22,5 – 20) ÷ 7 = 49,5 kN
Vérification : Σ Fy = 49,5 - 6 × 4 - 40 - 9 × 5 + 79,5 - 20 = 0 ⇒ OK!
(a) et (b) Déterminons les contraintes normale et de cisaillement maximales pour x = 2 m et pour x = 7m
La formule donnant la contrainte normale maximale est :
σ
> = M / S
Le module de flexion « S » de la poutre peut être lu directement dans le tableau F1:
Sx = 634 × 103 mm3 = 634 × 103 (10–3 m)3 = 634 × 103 × 10 –9 m3 = 634 × 10–6 m3
Pour obtenir la contrainte normale maximale pour une valeur donnée de x, il suffit donc d’y calculer M(x ), la valeur
du moment fléchissant.
La formule donnant la contrainte de cisaillement maximale est :
τ
> = 1,5 he
V dans laquelle
V = effort tranchant pour la section considérée.
0 1 5 7 8 10
RG RD
w2
w
1
F1 = 40,00 kN F2 = 20,0 kN
x
(
m
)
w1 = 6,0 kN/m
w2 = 9,0 kN/m
Fw1 = 24 kN Fw2 = 45 kN
W 310 × 45

203-001 D ch. 7 D7.5
h = hauteur du profilé = 313 mm = 0,313 m
e = épaisseur de l’âme du profilé = 6,6 mm = 0,0066 m (tableau F1)
On a donc τ
>
= 1,5 he
V = 1,5 )0066,0()313,0( ×
V = 726,11 V (en unités SI)
Pour obtenir la valeur de τ
> pour une valeur donnée de « x », il suffit donc d’y calculer l’effort tranchant.
(a) Il suffit donc de calculer M(x = 2), et V(x=2) pour x = 2 m.
M(x = 2 m), = RG
× (2 – 1) – w1 × 2 × 1 = 49 500×1 – 6 000×2 = 37 500 N.m
⇒ σ> (x = 2) = M(x = 2 m), / Sx = 37 500 ÷ (634 × 10–6) = 59,15 MPa
V(x = 2 m) = RG – w1 × 2 =49 500 – 6 000 × 2 = 49 500 – 12 000 = 37 500 N
⇒ τ
> (x = 2 m) = 726,11
× 37 500 = 27,229 × 106 Pa = 27,23 MPa
(b) Il suffit de calculer M(x = 7), et V(x=7) pour x = 7 m.
M(x = 7 m), = 49,5×6 – 24×5 – 9×2×1 – 40×4 = – 1 kNm = – 1 000 N.m
⇒ σ> (x = 7) = M(x = 7m), / Sx = ………………………………………. ……………….. = – 1,58 MPa
V(x = 7 m) = …………………………………………………………………………………………………..= –32 500 N
⇒ τ
> (x = 7 m) = ………………..…..
× …………..………… = ………..……….. × 106 Pa = 23,60 MPa
(c) Pour déterminer les contraintes normale et de cisaillement maximales pour toute la poutre, il suffit de calculer
respectivement « Mmax » et « Vmax », le moment fléchissant et l’effort tranchant maximaux pour toute la poutre. Pour
cela nous devons commencer par tracer le diagramme de l’effort tranchant. Nous pourrons facilement y lire la
valeur de Vmax. Pour obtenir la valeur de Mmax, il faudra commencer par déterminer les endroits où V = 0 et y
calculer la valeur de M. La valeur maximale obtenue pour M est Mmax. Dans chaque cas on ne tient pas compte du
signe.
N.B. : Le diagramme de V(x) est déjà tracé. Cependant vous devez calculer les surfaces sous la courbe permettant
d’obtenir la valeur de M(x) aux endroits désirés. Donc remplir chacune des cases blanches en y inscrivant la valeur
de la surface correspondante.