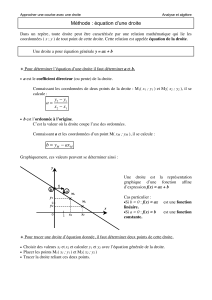
Exercice : MCC en régime transitoire
On considère un moteur à courant continu à aimants permanents dont les
caractéristiques sont les suivantes : tension d’induit : Un = 110 V, résistance
d’induit : R = 0,5 Ω, inductance d’induit : L = 75 mH, moment d’inertie de
l’ensemble mécanique en rotation : J = 1 kg · m2, couple de pertes mécaniques :
Cp = 0,7 Nm
1) La machine tournant à vide on mesure le courant absorbé par la machine : I0 =
1,8 A. En déduire le coefficient K vérifiant la relation C = K · I
2) En déduire également la vitesse de rotation à vide de la machine.
3) La machine tournant à vide depuis longtemps, on accouple brutalement (au
temps conventionnel t = 0) la charge mécanique représentant un couple résistant :
Cr = 13 Nm.
Écrire l’équation différentielle reliant les différents couples à la vitesse de rotation
Ω (rad/s) de la machine.
4) Écrire également la loi de maille électrique de la machine en régime transitoire
ainsi que les relations reliant les grandeurs électriques et mécaniques.
5) Former alors une équation globale reliant la vitesse Ω (rad/s), sa dérivée et la
dérivée du courant.
6) Qu’est-il possible de faire comme hypothèse permettant de simplifier cette
équation ?
(On considèrera que les évolutions des grandeurs électriques sont rapides devant
celles des évolutions mécaniques.) Utiliser la nouvelle équation trouvée pour
résoudre l’équation de la question 3 portant sur la vitesse. Représenter l’évolution
transitoire de la vitesse de la machine.
7) Quel est approximativement la durée du régime transitoire de la vitesse de la
machine lors d’un changement de charge ?
8) Calculer et représenter également l’évolution du courant d’induit i(t).
9) La machine étant revenue à vide depuis longtemps on couple (à t = 0) une charge
trop importante qui bloque le rotor. Calculer alors rapidement la valeur maximale
du courant lors du blocage et le temps nécessaire au courant pour atteindre cette
valeur.

À quelle valeur de courant doit-on approximativement fixer les seuils des
protections électriques ?
1
/
2
100%