Page 1
Institut Préparatoire aux Etudes d’ingénieurs de Nabeul
Série : Mécanique Quantique
Classes : SM, ST AU : 2016-2017
Exercice 1
Partie 1 : L'effet photoélectrique.
1°/ Rappeler et interpréter la relation
d'Einstein donnant le bilan énergétique de
l’absorption du photon par un métal.
2°/ a) Une substance métallique éclairée par
la lumière visible (0,4--0,75
m
) ne produit
aucun courant électrique. Que peut-on dire de
son travail de sortie?.
b) On recouvre la substance par du zinc dont
le travail de sortie est
3,4eV
s
W
puis on
l'éclaire avec une radiation de longueur d'onde
0,2 m
. Donner la longueur d'onde et la
fréquence du seuil photoélectrique. Quelle est
la vitesse maximale des photoélectrons
arrachés.
c) Mêmes questions pour le césium dont le
travail de sortie est
1,8eV
s
W
.
d) Comparer les résultats b) et c) et conclure.
On donne :
. 12400E eV A hc
et
19
1eV 1,6x10 J
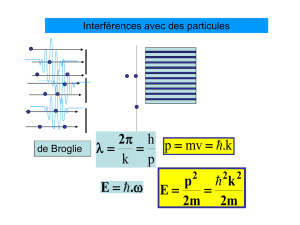
Partie 2 : Hypothèse de Louis De Broglie.
1°/ Rappeler et commenter cette hypothèse.
2°/ Calculer la longueur d'onde de L. De
Broglie associée à:
a) Une goutte d'eau de diamètre
0,1d mm
se déplaçant à la vitesse
10 m/sv
.
b) Un neutron thermique d'énergie cinétique
0,05
c
E eV
, (on donne :
2940mc Mev
).
c) Conclure.
Partie 3: Inégalités de Heisenberg.
1°/ Si l'on suppose que le rayon de l'orbite de
Bohr
00,529aA
est connu à 1% près,
calculer
v
incertitude sur la vitesse de
l'électron de masse 9,1 10-31Kg. Conclusion ?
2°/ Si l'on suppose que la position d'une bille
de masse 1 g est connue au
m
près, quelle
est l'incertitude sur sa vitesse ? Conclusion ?
3°/ Un automobiliste féru de mécanique
quantique à été pris par un radar à 120 Km/h
au volant de sa voiture de 1500 Kg. Il invoque
le principe d'incertitude d'Heisenberg pour
contester le P.V. A-t-il raison ?
Exercice 2 : Paquet d’ondes.
On considère une particule libre de masse
m
que l'on décrit par un paquet d’ondes (à une
dimension) défini par :
1
,2
j kx k t
x t g k e dk
On considère l’instant
0t
et on suppose que
gk
a une forme rectangulaire :
12
1 pour
0 ailleurs
k k k
gk
1°/ a) Déterminer
,0x
, on posera
12
02
kk
k
et
21
k k k
.
b) En déduire la densité de probabilité et tracer sa variation.
c) Justifier que l’onde
,0x
peut être associée à la particule.
2°/ Quel est le produit
xk
des extensions des fonctions. Réécrire ce produit en utilisant la relation
de L. De Broglie. Commenter.
3°/ Donner la relation de dispersion
k
. Comparer la vitesse de groupe
g
v
à la vitesse de phase
v
et à la vitesse
v
de la particule. Conclure.
4°/ On plonge maintenant la particule dans un potentiel constant
0
U x U
, montrer que
l'expression générale
,xt
du paquet d'ondes est solution de l'équation de Schrödinger.
Page 2
Exercice 3 : Puits de potentiel.
Soit une particule de masse
m
d'énergie
E
se trouve piégée dans un puits de potentiel carré de la
figure ci-contre tel que
0
0EV
.
1°/
0
V
: fini
a) Résoudre l'équation de Schrödinger
stationnaire dans les trois régions.
b) Donner la signification physique de chaque
terme.
c) Expliciter les conditions de continuités aux
points
0x
et
xa
.
d) Déduire la condition à la quelle doivent
satisfaire les quantités :
k
,
et
a
, où
k
et
sont définies comme suit:
22
2mE
k
et
0
22
2m V E
.
2)
0
V
infini
Si
0
V
tend vers l'infini :
a) Que deviennent les solutions de l'équation
de Schrödinger dans les régions (I) et (III)?
b) En écrivant les conditions de continuité
aux points
0x
et
xa
, déduire les valeurs
possibles de l'énergie
E
de la particule dans
le puits. Conclure.
Exercice 4 : Marche de potentiel.
On considère la marche de potentiel de la figure au-dessous :
1°/ Donner des situations physiques
correspondant à cette situation.
2°/ Une particule de masse
m
et d’énergie
E
est envoyée depuis
x
. Que peut-il se
passer d’un point de vue classique ?
On s’intéresse pour la suite à la situation
quantique. On suppose dans la un premier
temps que l’énergie
EV
.
3°/ a) Donner l’expression de la fonction
d’onde stationnaire dans les différentes zones
0x
et
0x
, puis commenter les résultats.
On posera
2mE
k
et
2
'm E V
k
.
b) Quelles relations de continuité peut-on
utiliser ?
4°/ a) En déduire l’expression du coefficient
de probabilité en réflexion
R
et en
transmission
T
.
b) Commenter les résultats précédents.
5°/ Reprendre les questions précédentes pour
EV
. On posera
2
'm V E
k
.
1
/
2
100%
