fiche bode

Fiches pratiques - poujouly.net Page 1 sur 2 S.POUJOULY
Fiches pratiques Systèmes linéaires - Asservissement #Bode
poujouly.net
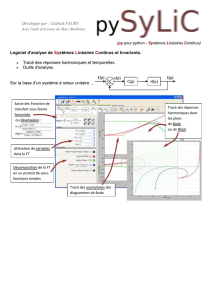
Diagramme de Bode
@poujouly
Les formes canoniques du 1er ordre
π/2
0
ωo
ω
ω
Gain
Phase
+20dB/dec
0dB
Tracé réel
−π/2
0
ωo
ω
ω
Gain
Phase
-20dB/dec
0dB
Tracé réel
−π
0
ωω
Gain Phase
20.log(|K|)
0dB
Tracé réel
Si K > 0
Si K < 0
20.log(|K|) Si |K| > 1
Si |K| < 1
π/2
0ωo
ωo
ω
ω
Gain
Phase
+20dB/dec
π/4
0dB
3dB
Tracé asymptotique
Tracé réel
-π/2
0ωo
ωo
ω
ω
Gain
Phase
-20dB/dec
-π/4
0dB
-3dB
Tracé asymptotique
Tracé réel
o
p
1
1
ω
+
o
p
1ω +
o
p
ω
p
o
o
p
1ω
=
ω
K

Fiches pratiques - poujouly.net Page 2 sur 2 S.POUJOULY
A propos du diagramme de Bode
Il s’agit d’une représentation très utilisée en électronique permettant de tracer le gain (dB) et l’argument (ou
phase) d’une fonction de transfert en fonction de la fréquence. Pour l’axe de la fréquence on choisit une échelle
logarithmique permettant d’obtenir une représentation compacte pour une grande dynamique.
Hendrik Wade Bode
(24/12/1905- 22/06/1982) ingénieur, chercheur et
inventeur américain d’origine néerlandaise.
Intérêt majeur des diagrammes de Bode
 Le diagramme de Bode permet de fournir une indication sur la réponse fréquentielle d’une fonction de
transfert d'un système linéaire (filtre, etc..) pour une très grande dynamique.
 L’intérêt majeur réside dans sa construction : Une fonction de transfert se décompose traditionnellement en
produit de fonction de transfert élémentaires (ou canoniques). Le tracé du diagramme de Bode est alors obtenu
en effectuant une somme graphique de chaque gain et chaque phase (ou argument) des fonctions de transferts
élémentaires composant la fonction de transfert du système étudié.
Exemple : Fonction de transfert sous la forme d’un produit de fonction de transfert élémentaire
)p(T)p(T)p(T)p(T
321
⋅
⋅
=
Le calcul du gain nous donne )j(T)j(T)j(T)j(T
321
ω⋅ω⋅ω=ω
donc
(
)
(
)
(
)
(
)
)j(Tlog20)j(Tlog20)j(Tlog20)j(Tlog20G
321dB
ω⋅+ω⋅+ω⋅=ω⋅=
dB3dB2dB1dB
GGGG ++=
(
)
(
)
(
)
(
)
)p(TArg)p(TArg)p(TArg)p(TArg
321
++=
1 2 10 20 5 50 100 200 500 1k
f
log(f)
Gain (dB) et/ou Phase (degré ou radian) « papier semi-log »
Tracé diag. de Bode total =
Somme graphique de chaque
diag. de Bode élémentaire