Calcul des Ressorts

ESIM Département : Génie Mécanique
Conception de Machines 109
Chapitre 11
CALCUL DES RESSORTS
I- CLASSIFICATION DES RESSORTS
Les ressorts sont classés à partir de la sollicitation reçue. Le matériau travaille soit en torsion, soit
en flexion. La sollictation du ressort n’est pas nécessairement la même que celle du matériau.
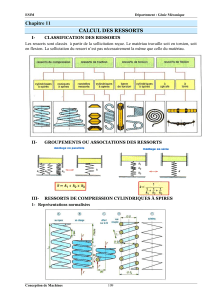
II- GROUPEMENTS OU ASSOCIATIONS DES RESSORTS
III- RESSORTS DE COMPRESSION CYLINDRIQUES À SPIRES
1- Représentations normalisées

ESIM Département : Génie Mécanique
Conception de Machines 110
2- Hypothèses des calculs
Le calcul est relatif à un ressort hélicoïdal à fil rond travaillant sous l’effet de deux forces
directement opposées.
- Le fil enroulé supporte un couple de torsion : Mt = F . D/2
- La force exercée sur le ressort est concentrée. (Spires meulées)
- Les forces d’appui sont perpendiculaires à l’axe du ressort.
- Condition d’encombrement : 5 ≤ D/d ≤ 10.
- Choisir le pas tel que la pente de l’hélice doit être inférieure à 1/8.
8
1
2
Pas
tgi
3- Formules utilisées
3
...8 dDF
Max
Contrainte
4
3
....8 dG nDF
fu
Flèche
3
4
..8 .Dn dG
f
F
K
u
Raideur
4- Détermination du ressort
On a deux formules mettant en relation les inconnus ζadm ; F ; D ; d ; f ; G ; nu ; et déterminer le
ressort, c'est-à-dire connaître ces caractéristiques.
ζadm et G sont caractéristiques du matériau.
F : généralement donné ou calculé.
Il nous reste deux équations avec quatre inconnus, et par conséquent il faut faire un calcul
d’approche à partir de deux relations, tout en vérifiant les hypothèses.
5- Méthode pratique
Dresser le tableau suivant :
d
D
D/d
fMax/spire
Pas
Pente = tg i
nu
L0
?
?
?
4
3
...8 dG DF
fMax/spire + 1.1 d
8
1
D
Pas
Pas dL 5.1
0
ou
spireMax
total
ff
/
dPasnu5.1. 
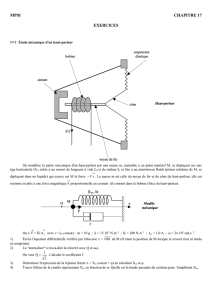
6- Application : (Embrayage)
L’effort presseur sur les disques d’un embrayage à friction plane est obtenu par 12 ressorts
hélicoïdaux. Cet effort presseur de densité 5470N ; permet une déformation de ressort de 15mm.
Les ressorts sont de caractéristiques mécaniques identiques avec :
τMax adm = 70 daN/mm2 ; G = 80.103 N/mm2
Déterminer les autres caractéristiques.

ESIM Département : Génie Mécanique
Conception de Machines 111
7- Résolution
Données:
ressortsnu12
;
NNtotal 5470
;
mmftotal 15
2
/700 mmN
adm 
;
23 /10.80 mmNG 
Condition de résistance:
admMax
adm
dDF
3
...8
(1)
Flèche maximale (ou flèche total) :
mmn
dG DF
futotal 15
...8 4
3
(2)
Condition d’encombrement :
dDd 105
(3)
Soit F l’effort appliqué par un seul ressort :
N
N
Ftotal 83,455
12
5470
12 
D’où (1) donne :
3
.8 .d F
Dadm
3
83,4558700 dD 
D’après (3) on a : et
Traçage des courbes :
3
603,0
5
dD
dD
3
603,05 dd 
603,0 5
2d
mmd88,2
603,0 5
Diamètre normalisé ≥ 2,88mm choix : d = 3 mm. D’où :
mmD28,163603,0 3
Compléter le tableau :
d
D
D/d
fMax/spire
Pas
Pente = tg i
nu
L0
3
16,28
5,42
2,39
5,69
Normalisé : 6
125,011,0 
6 ,27
Choix : 6.5
43,5
Remarques :
 Le nombre des spires doit être un nombre impaire et multiple de 0.5.
 Le pas doit être normalisé.
3
603,0 dD 
dD 5
dD 10
d
dmin