modeliser-une-situation-spatiale

Modéliser une situation
spatiale

I. Section d’un prisme droit
par un plan
Cas particulier du parallélépipède rectangle
•La section d’un prisme droit par un plan parallèle à la base
est un polygone de mêmes dimensions que la base.
•La section d’un prisme droit par un plan parallèle à une arête
latérale est un rectangle dont une dimension est la longueur
de l’arête.
Plan parallèle à la base Plan parallèle à une arête
Dans les deux cas la section est un rectangle

II. Section d’un cylindre par un plan
Plan parallèle à la base Plan parallèle à son axe
La section est un cercle de
même rayon que la base.
La section est un rectangle
dont l’une des dimensions
est la hauteur du cylindre.

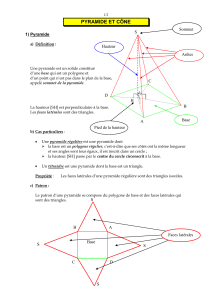
III.Section d’un cône et d’une
pyramide par un plan
Section d’un cône Section d’une pyramide
La section est un cercle qui
est une réduction du cercle
de base.
La section est un polygone
qui est une réduction du
polygone de base.
SO' SA' O'A'
SO SA OA
SH' SA' SB' H'A' ...
SH SA SB HA

S
O' A'
Exemple:
Le triangle SOA rectangle en O
engendre un cône de révolution de
hauteur 20 cm et de rayon de base
6cm.
On réalise la section de ce cône par
le plan parallèle à la base passant par
O', un point de [SO], tel que
SO' = 2 cm.
OA
S
O' A'